
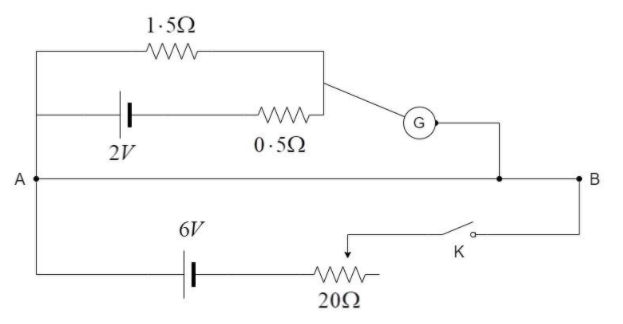
In Fig. AB is 300cm long wire having resistance $10\Omega $per meter. Rheostat is set at $20\Omega $. The balance point will be attained at
A. 1.0m
B. 1.25m
C. 1.5m
D. Cannot be determined

Answer
554.1k+ views
Hint: The circuit provided in the question is that of a device known as potentiometer. This problem can be solved by understanding the basic principle of potentiometer i.e. the voltage across the resistance is directly proportional to the length at which the galvanometer reads null deflection.
$V \propto l$
$V = kl$
where k = voltage gradient of the potentiometer.
Complete step by step answer:
Potentiometer is a device used to calculate the emf and internal resistance of unknown cells by comparing them using a known value. It is loosely based on the principles of metre bridge, which is used to calculate the unknown resistances using the Wheatstone’s network.
It consists of a uniform wire AB, usually made of constantan. A steady current is maintained at one end of the wire AB and the other end is connected to the cells in study as shown in the circuit diagram below:
The potential gradient of the potentiometer is a constant value. It is taken as a standard reference to calculate the emf and internal resistance on the other end of the circuit. The voltage on the other end of the circuit is given by –
$V = KL$
where K = potential gradient and L = length at which null point occurs.
To calculate potential gradient:
The potential gradient is calculated by finding the voltage across the wire AB and dividing it by the length of AB i.e., 300cm which is equal to 3m.
The net resistance of AB, ${R_{AB}}$ = Length of AB $ \times $ Resistance per unit length = $10 \times 3 = 30\Omega $
Given, ${\varepsilon _0} = 6V$
Net resistance in the lower circuit, ${R_{net}} = R + {R_{AB}} = 20 + 30 = 50\Omega $
Current in the upper circuit, $I = \dfrac{{{\varepsilon _0}}}{{{R_{net}}}} = \dfrac{6}{{50}} = 0 \cdot 12A$
Hence, voltage drop across AB, ${V_{AB}} = I{R_{AB}} = 0 \cdot 12 \times 30 = 3 \cdot 6V$
Given the length of AB, $l = 3m$, the potential gradient of the wire,
$K = \dfrac{{{V_{AB}}}}{l} = \dfrac{{3 \cdot 6}}{3} = 1 \cdot 2V{m^{ - 1}}$
Using the value of potential gradient, we can find the balance point in the upper part of the circuit, as follows:
The terminal voltage in the upper circuit is given by, $V = \dfrac{{2 \times 1 \cdot 5}}{2} = 1 \cdot 5V$
By applying this in the equation for voltage of the potentiometer, we have –
$V = K{l_a}$
where ${l_a}$= required balancing length where the galvanometer shows zero deflection.
Substituting the values, we have –
$1 \cdot 5 = 1 \cdot 2{l_a}$
$ \Rightarrow {l_a} = \dfrac{{1 \cdot 5}}{{1 \cdot 2}} = 1 \cdot 25m$
Hence, the correct answer is option (B).
Note: The reason for using constantan wire is, because the rate of change of resistivity per rise in temperature is very low. Hence, the resistance of the wire remains constant at a wide range of operating temperatures and gives accurate results.
$V \propto l$
$V = kl$
where k = voltage gradient of the potentiometer.
Complete step by step answer:
Potentiometer is a device used to calculate the emf and internal resistance of unknown cells by comparing them using a known value. It is loosely based on the principles of metre bridge, which is used to calculate the unknown resistances using the Wheatstone’s network.
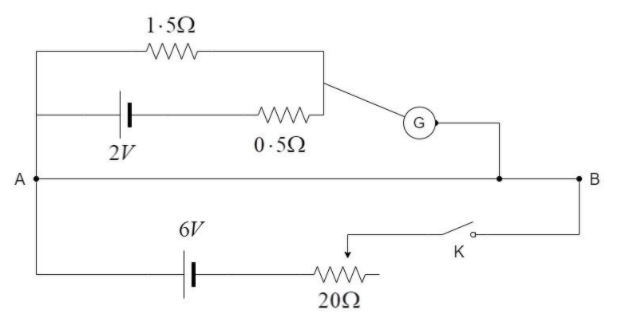
It consists of a uniform wire AB, usually made of constantan. A steady current is maintained at one end of the wire AB and the other end is connected to the cells in study as shown in the circuit diagram below:

The potential gradient of the potentiometer is a constant value. It is taken as a standard reference to calculate the emf and internal resistance on the other end of the circuit. The voltage on the other end of the circuit is given by –
$V = KL$
where K = potential gradient and L = length at which null point occurs.
To calculate potential gradient:
The potential gradient is calculated by finding the voltage across the wire AB and dividing it by the length of AB i.e., 300cm which is equal to 3m.
The net resistance of AB, ${R_{AB}}$ = Length of AB $ \times $ Resistance per unit length = $10 \times 3 = 30\Omega $
Given, ${\varepsilon _0} = 6V$
Net resistance in the lower circuit, ${R_{net}} = R + {R_{AB}} = 20 + 30 = 50\Omega $
Current in the upper circuit, $I = \dfrac{{{\varepsilon _0}}}{{{R_{net}}}} = \dfrac{6}{{50}} = 0 \cdot 12A$
Hence, voltage drop across AB, ${V_{AB}} = I{R_{AB}} = 0 \cdot 12 \times 30 = 3 \cdot 6V$
Given the length of AB, $l = 3m$, the potential gradient of the wire,
$K = \dfrac{{{V_{AB}}}}{l} = \dfrac{{3 \cdot 6}}{3} = 1 \cdot 2V{m^{ - 1}}$
Using the value of potential gradient, we can find the balance point in the upper part of the circuit, as follows:
The terminal voltage in the upper circuit is given by, $V = \dfrac{{2 \times 1 \cdot 5}}{2} = 1 \cdot 5V$
By applying this in the equation for voltage of the potentiometer, we have –
$V = K{l_a}$
where ${l_a}$= required balancing length where the galvanometer shows zero deflection.
Substituting the values, we have –
$1 \cdot 5 = 1 \cdot 2{l_a}$
$ \Rightarrow {l_a} = \dfrac{{1 \cdot 5}}{{1 \cdot 2}} = 1 \cdot 25m$
Hence, the correct answer is option (B).
Note: The reason for using constantan wire is, because the rate of change of resistivity per rise in temperature is very low. Hence, the resistance of the wire remains constant at a wide range of operating temperatures and gives accurate results.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




