Question

In case of simple harmonic motion, if the velocity is plotted along the X-axis and the displacement (from the equilibrium position) is plotted along the Y-axis, the resultant curve happens to be an ellipse with the ratio:
\[\dfrac{{majoraxis(alongX)}}{{\min oraxis(alongY)}} = 20\pi \]. What is the frequency of the simple harmonic motion?
A) \[\left( {\text{A}} \right){\text{ }}100Hz\]
B) \[\left( {\text{B}} \right){\text{ }}20Hz\]
C) \[\left( {\text{C}} \right){\text{ }}10Hz\]
D) \[\left( {\text{D}} \right){\text{ }}\dfrac{1}{{10}}Hz\]

Answer 1

Hint:First we have to assume the variables on the given data.
Then we defined the simple harmonic function and found the velocity by using the elliptical curve on the velocity displacement graph.
Finally we get the frequency of the simple harmonic function.

Complete step by step answer:
In case of Simple harmonic motion(S.M.H) be M,
Let $V$ is the velocity and displacement from equilibrium position is $x$ .
The displacement from equilibrium position is defined as a function of time $t$,
 We can write it as,\[x = A\sin \omega t\].
Here, \[A\]= Amplitude of the S.H.M and \[\omega \]= Angular frequency = \[2\pi \times {\text{frequency}}\]
The velocity of the S.H.M is calculated by differentiating the displacement,
\[V = \dfrac{{dx}}{{dt}}\]=\[A\omega \cos \omega t\].
Now we know an elliptical equation in X-Y axis should be,
\[\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1\] .
The elliptical equation diagram is as follows,

where, the major axis =\[2a\] and the minor axis = \[2b\].
Here, The velocity is plotted along X-axis and the displacement is plotted along Y-axis, and the resultant curve is an ellipse as the figure drawn is as follows:

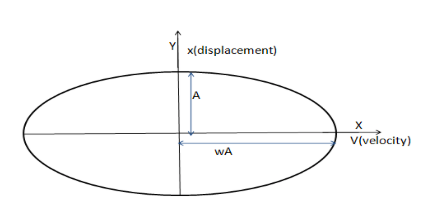
Therefore, \[\dfrac{{{V^2}}}{{{A^2}{\omega ^2}}} + \dfrac{{{x^2}}}{{{A^2}}} = 1\] - Elliptical equation.
Here the major axis is $2\omega A$ and the minor axis is $2A$ .
In this question stated as, \[\dfrac{{majoraxis(alongX)}}{{\min oraxis(alongY)}} = 20\pi \]
Putting the values an we get,
\[ \Rightarrow \dfrac{{2\omega A}}{{2A}} = 20\pi \]
Cancelling the same term we get,
\[ \Rightarrow \omega = 20\pi \]
Now, we have to find out the frequency.
\[\omega = 2\pi \times {\text{frequency}}\]
\[ \Rightarrow \omega = 2\pi \times f\]
Let us take the \[f\] as LHS and remaining as in divide term we get
\[ \Rightarrow f = \dfrac{\omega }{{2\pi }}\]
Putting the value of \[\omega \]and we get,
\[ \Rightarrow f = \dfrac{{20\pi }}{{2\pi }}\]
On divide the term we get,
\[ \Rightarrow f = 10\]
Therefore the frequency is \[f = 10Hz\].

Hence, the right answer is in option (C).

Note: In the case of an S.H.M of a particle if the displacement from the equilibrium position is $x$,
Here \[\dfrac{{dx}}{{dt}}\] is the change in displacement per unit time which defines the Velocity of that particle.
If we represent the displacement as,\[x = A\sin \omega t\]
The velocity should be, \[V = \dfrac{{dx}}{{dt}} = \omega A\cos \omega t\]
\[ \Rightarrow V = \omega A\sin (\omega t + \dfrac{\pi }{2})\]
Hence, the phase difference between the displacement and velocity of a particle in S.H.M is \[\dfrac{\pi }{2}\].