Question

In an experiment using tangent galvanometer, the magnetic induction is measured at various points on the axis of a current carrying circular coil on both sides of the center O of the coil. The variation of magnetic field along the axis is best represented in the curve:
A.

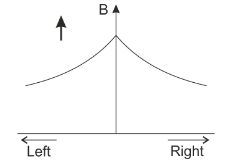
B.

C.

D.

Answer 1

Hint: In a current carrying coil the electric current creates a magnetic field which is more concentrated in the center of the coil than outside the loop. According to Biot-Savart’s law, the magnetic field at a point due to an element of a conductor carrying current is,
-Directly proportional to the strength of the current.
-Directly proportional to the length of the element.
-Directly proportional to the Sine of the angle between the element and the line joining the element to the point.
-Inversely proportional to the square of the distance between the element and the point.

Complete step by step answer:
Let us assume that the radius of the coil be R.
Then the magnetic field at distance r on the axis of coil is given by,
$B = \dfrac{{{\mu _o}I{R^2}}}{{2{{({r^2} + {R^2})}^{\dfrac{3}{2}}}}}$
Now when $r > > R$
$B = \dfrac{{{\mu _o}I{R^2}}}{{2{r^3}}}$
Since radius of the coil and current are constant we can say that,
$B \propto \dfrac{1}{{{r^3}}}......(1)$
Now at the center of the coil we have,
$r = R$
Hence, the expression for magnetic field becomes
$
B = \dfrac{{{\mu _o}I{r^2}}}{{{r^3}}} \\
\Rightarrow B = \dfrac{{{\mu _o}I}}{r} \\ $
Since, current is constant Therefore, we have
$B \propto \dfrac{1}{r}......(2)$
From (1) and (2) we can observe that the plot for magnetic field due to current carrying coil is
\[\begin{array}{*{20}{c}}
B& \propto &{\left\{ {\begin{array}{*{20}{c}}
{\dfrac{1}{{{r^3}}}}&{r > > R} \\
{\dfrac{1}{r}}&{r = R}
\end{array}} \right\}}
\end{array}\]
It is clear from the above equations that option B is the correct representation.

Note:When a current flows in a wire, it creates a circular magnetic field around the wire. This magnetic field can deflect the needle of a magnetic compass. The strength of a magnetic field is directly proportional to the current flowing. Therefore, if an alternating current is flowing, a magnetic field around the conductor will be produced, that is in phase with the alternating current.