Question

In a half-wave rectifier, the r.m.s value of the a.c component of the wave is
${\text{(a) equal to the dc value}} $
${\text{(b) more than the dc value}} $
${\text{(c) less than the dc value}} $
${\text{(d) zero}} $

Answer 1

Hint – In this question consider a sinusoidal equation of voltage that is $V = {V_m}\sin \omega t$, the dc voltage can be written as ${V_{D.C}} = \dfrac{{{V_m}}}{\pi }$ and the r.m.s value can be written as \[{V_{r.m.s}} = \sqrt {{{\left( {\dfrac{{{V_m}}}{{\sqrt 2 }}} \right)}^2}} \]. Use these to get the relation between the r.m.s value and the dc value.

Formula used: ${V_{D.C}} = \dfrac{{{V_m}}}{\pi }$, \[{V_{r.m.s}} = \sqrt {{{\left( {\dfrac{{{V_m}}}{{\sqrt 2 }}} \right)}^2}} \]

Complete step-by-step solution -

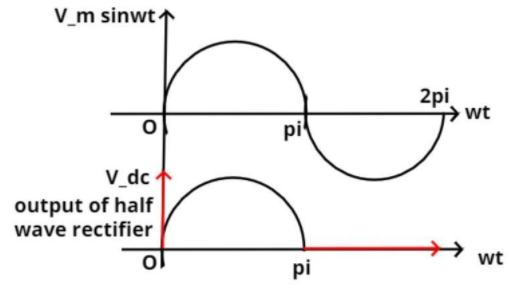
Let the sinusoidal voltage be
$V = {V_m}\sin \omega t$, where ${V_m}$ is maximum component of voltage and $\omega $ is the frequency.
Now as we know that the above signal is A.C single so the D.C component of this signal is zero.
But when we use half wave rectifier A.C signal is converted into D.C signal and the value of D.C voltage is
$ \Rightarrow {V_{D.C}} = \dfrac{{{V_m}}}{\pi }$volts.
And the r.m.s value of this A.C component is
\[ \Rightarrow {V_{r.m.s}} = \sqrt {{{\left( {\dfrac{{{V_m}}}{{\sqrt 2 }}} \right)}^2}} = \dfrac{{{V_m}}}{{\sqrt 2 }}\] volts.
So as we see that $\dfrac{{{V_m}}}{{\sqrt 2 }} > \dfrac{{{V_m}}}{\pi }$
Therefore, ${V_{r.m.s.}} > {V_{D.C}}$
So the r.m.s value of the A.C component of the wave is more than the D.C value.
So this is the required answer.
Hence option (B) is the required answer.

Note – A half wave rectifier is a rectifier that allows only one half cycle of an A.C voltage to pass through it, the diode present in the circuitry of half-wave rectifier is designed in such a way that it automatically gets reversed biased as soon as the negative half-cycle is passed through the input of the circuit.