Question

If the vector \[6{\text{i - 3j - 6k}}\] is decomposed into vectors parallel and perpendicular to the vector ${\text{i + j + k}}$ then find the vectors.
A) $ - \left( {{\text{i + j + k}}} \right)$& ${\text{7i - 2j - 5k}}$
B)$ - 2\left( {{\text{i + j + k}}} \right)$ & ${\text{i - j - 4k}}$
C)$2\left( {{\text{i + j + k}}} \right)$ & ${\text{4i - 5j - 8k}}$
D) $3\left( {{\text{i + j + k}}} \right)$ & ${\text{i - j + k}}$

Answer 1

Hint: A vector is decomposed into two vectors (say ‘x’ and ‘y’) which are parallel and perpendicular to the vector ${\text{i + j + k}}$. We can write x=m$\left( {{\text{i + j + k}}} \right)$ where m is a scalar quantity as c is parallel to${\text{i + j + k}}$. And y is perpendicular to it so their dot product will be zero. Assume d to be ${{\text{a}}_1}{\text{i + }}{{\text{a}}_2}{\text{j + }}{{\text{a}}_3}{\text{k}}$ where ${{\text{a}}_1} + {{\text{a}}_2} + {{\text{a}}_3} = 0$ . Now add the value of ‘x’ and ‘y’ and equate it to a given vector (\[6{\text{i - 3j - 6k}}\]). Solve and find the vectors.

Complete step-by-step answer:
The given vector is=\[6{\text{i - 3j - 6k}}\] which is decomposed into two vectors such that they are parallel and perpendicular to the vector${\text{i + j + k}}$. Let us assume the two vectors to be x and y . Then we can write- \[6{\text{i - 3j - 6k}}\]=x + y --- (i)

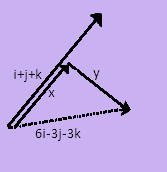
Here given that x is parallel to ${\text{i + j + k}}$ so x= m$\left( {{\text{i + j + k}}} \right)$ where m is scalar.
Also given, y is perpendicular to ${\text{i + j + k}}$ so their dot product will be zero. Assume y=${{\text{a}}_1}{\text{i + }}{{\text{a}}_2}{\text{j + }}{{\text{a}}_3}{\text{k}}$ where${{\text{a}}_1} + {{\text{a}}_2} + {{\text{a}}_3} = 0$. Now we put the values of x and y in eq. (i).
$ \Rightarrow 6{\text{i - 3j - 6k = m}}\left( {{\text{i + j + k}}} \right) + {{\text{a}}_1}{\text{i + }}{{\text{a}}_2}{\text{j + }}{{\text{a}}_3}{\text{k}}$
On multiplying m with the vectors and separating the common vectors we get,
 \[
   \Rightarrow 6{\text{i - 3j - 6k = mi + mj + mk}} + {{\text{a}}_1}{\text{i + }}{{\text{a}}_2}{\text{j + }}{{\text{a}}_3}{\text{k}} \\
   \Rightarrow 6{\text{i - 3j - 6k = mi}} + {{\text{a}}_1}{\text{i + mj}} + {{\text{a}}_2}{\text{j + mk}} + {{\text{a}}_3}{\text{k}} \\
 \]
Now taking i, j and k common, we get-
$ \Rightarrow 6{\text{i - 3j - 6k = }}\left( {{\text{m}} + {{\text{a}}_1}} \right){\text{i + }}\left( {{\text{m + }}{{\text{a}}_2}} \right){\text{j + }}\left( {{\text{m + }}{{\text{a}}_3}} \right){\text{k}}$
On comparing the coefficient of i, j and k, we get
$
   \Rightarrow 6 = {\text{m}} + {{\text{a}}_1} \\
   \Rightarrow - 3 = {\text{m}} + {{\text{a}}_2} \\
   \Rightarrow - 6 = {\text{m}} + {{\text{a}}_3} \\
    \\
 $
On adding the three values we get,
\[ \Rightarrow 3{\text{m + }}{{\text{a}}_1} + {{\text{a}}_2} + {{\text{a}}_3} = 6 - 3 - 6 = - 3\]
We also know that ${{\text{a}}_1} + {{\text{a}}_2} + {{\text{a}}_3} = 0$. So putting this value, we get the value of m,
$ \Rightarrow 3{\text{m}} = - 3 \Rightarrow {\text{m}} = - 1$
Now we know the value of m so we can find the value of ${{\text{a}}_1},{{\text{a}}_2}$ and ${{\text{a}}_3}$ ,
$
   \Rightarrow {{\text{a}}_1} = 6 + 1 = 5 \\
   \Rightarrow {{\text{a}}_2} = - 3 + 1 = - 2 \\
   \Rightarrow {{\text{a}}_3} = - 6 + 1 = - 5 \\
 $
So putting these values in eq. (i) we get-
$ \Rightarrow 6{\text{i - 3j - 6k}} = - 1\left( {{\text{i + j + k}}} \right) + \left( {{\text{7i - 2j - 5k}}} \right)$
Hence option ‘A’ is the correct answer.

Note: Here, the student may get confused that how ${{\text{a}}_1} + {{\text{a}}_2} + {{\text{a}}_3} = 0$. So remember we said that since y is perpendicular to ${\text{i + j + k}}$ so their dot product will be zero. And here, we assumed that y=${{\text{a}}_1}{\text{i + }}{{\text{a}}_2}{\text{j + }}{{\text{a}}_3}{\text{k}}$.
So $\left( {{{\text{a}}_1}{\text{i + }}{{\text{a}}_2}{\text{j + }}{{\text{a}}_3}{\text{k}}} \right).\left( {{\text{i + j + k}}} \right) = 0$
We will multiply the coefficient of i, j and k.
$ \Rightarrow \left( {{{\text{a}}_1} \times 1} \right) + \left( {{{\text{a}}_2} \times 1} \right) + \left( {{{\text{a}}_3} \times 1} \right) = 0$
Which means that ${{\text{a}}_1} + {{\text{a}}_2} + {{\text{a}}_3} = 0$.