
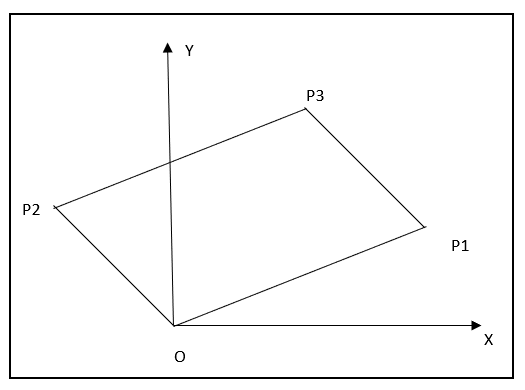
If the points ${{P}_{1}}$ and ${{P}_{2}}$ represent two complex numbers ${{z}_{1}}$ and ${{z}_{2}}$, then the point ${{P}_{3}}$ represents
A. ${{z}_{1}}+{{z}_{2}}$
B. ${{z}_{1}}-{{z}_{2}}$
C. ${{z}_{1}}\times {{z}_{2}}$
D. ${{z}_{1}}\div {{z}_{2}}$
Answer
232.8k+ views
Hint: In this question, we have to find the complex number at point ${{P}_{3}}$. For this, the property of parallelogram i.e., the midpoints of the diagonals of a parallelogram are equal is used.
Formula Used: The complex number $(x,y)$ is represented by $x+iy$.
If $z=x+iy\in C$, then $x$ is called the real part and $y$ is called the imaginary part of $z$. These are represented by $\operatorname{Re}(z)$ and $\operatorname{Im}(z)$ respectively.
$z=x+iy$ be a complex number such that $\left| z \right|=r$ and $\theta $ be the amplitude of $z$. So, $\cos \theta =\dfrac{x}{r},\sin \theta =\dfrac{b}{r}$
And we can write the magnitude as
$\begin{align}
& \left| z \right|=\left| x+iy \right| \\
& \Rightarrow r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
\end{align}$
Thus, we can write
$z=x+iy=r\cos \theta +ir\sin \theta =r(\cos \theta +i\sin \theta )$
This is said to be the mod amplitude form or the polar form of $z$.
Where $\cos \theta +i\sin \theta $ is denoted by $cis\theta $ and the Euler’s formula is $\cos \theta +i\sin \theta ={{e}^{i\theta }}$
Complete step by step solution: Given that,
The points ${{P}_{1}}$ and ${{P}_{2}}$ are represented by the complex numbers ${{z}_{1}}$ and ${{z}_{2}}$.
These are the vertices of the given parallelogram $O{{P}_{1}}{{P}_{2}}{{P}_{3}}$
So, the midpoints of its diagonals are equal. I.e.,
${{P}_{1}}{{P}_{2}}=O{{P}_{3}}$
The midpoint of ${{P}_{1}}{{P}_{2}}$ is
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\text{ }...(1)$
The midpoint of $O{{P}_{3}}$ is
$\left( \dfrac{0+x}{2},\dfrac{0+y}{2} \right)\text{ }...(2)$
On equating (1) and (2), we get
\[{{P}_{3}}(x,y)=({{x}_{1}}+{{x}_{2}},{{y}_{1}}+{{y}_{2}})\]
Thus, this point is represented in the complex form as
$\begin{align}
& ({{x}_{1}}+{{x}_{2}},{{y}_{1}}+{{y}_{2}})=({{x}_{1}}+{{x}_{2}})+i({{y}_{1}}+{{y}_{2}}) \\
& \Rightarrow ({{x}_{1}}+i{{y}_{1}})+({{x}_{2}}+i{{y}_{2}}) \\
& \Rightarrow {{z}_{1}}+{{z}_{2}} \\
\end{align}$
Thus, the point ${{P}_{3}}$ is represented by ${{z}_{1}}+{{z}_{2}}$.
Option ‘A’ is correct
Note: Here we need to remember that, the required point is one of the vertices of the given parallelogram. So, the property of the parallelogram is applied to find the required vertex.
Formula Used: The complex number $(x,y)$ is represented by $x+iy$.
If $z=x+iy\in C$, then $x$ is called the real part and $y$ is called the imaginary part of $z$. These are represented by $\operatorname{Re}(z)$ and $\operatorname{Im}(z)$ respectively.
$z=x+iy$ be a complex number such that $\left| z \right|=r$ and $\theta $ be the amplitude of $z$. So, $\cos \theta =\dfrac{x}{r},\sin \theta =\dfrac{b}{r}$
And we can write the magnitude as
$\begin{align}
& \left| z \right|=\left| x+iy \right| \\
& \Rightarrow r=\sqrt{{{x}^{2}}+{{y}^{2}}} \\
\end{align}$
Thus, we can write
$z=x+iy=r\cos \theta +ir\sin \theta =r(\cos \theta +i\sin \theta )$
This is said to be the mod amplitude form or the polar form of $z$.
Where $\cos \theta +i\sin \theta $ is denoted by $cis\theta $ and the Euler’s formula is $\cos \theta +i\sin \theta ={{e}^{i\theta }}$
Complete step by step solution: Given that,
The points ${{P}_{1}}$ and ${{P}_{2}}$ are represented by the complex numbers ${{z}_{1}}$ and ${{z}_{2}}$.
These are the vertices of the given parallelogram $O{{P}_{1}}{{P}_{2}}{{P}_{3}}$
So, the midpoints of its diagonals are equal. I.e.,
${{P}_{1}}{{P}_{2}}=O{{P}_{3}}$
The midpoint of ${{P}_{1}}{{P}_{2}}$ is
$\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)\text{ }...(1)$
The midpoint of $O{{P}_{3}}$ is
$\left( \dfrac{0+x}{2},\dfrac{0+y}{2} \right)\text{ }...(2)$
On equating (1) and (2), we get
\[{{P}_{3}}(x,y)=({{x}_{1}}+{{x}_{2}},{{y}_{1}}+{{y}_{2}})\]
Thus, this point is represented in the complex form as
$\begin{align}
& ({{x}_{1}}+{{x}_{2}},{{y}_{1}}+{{y}_{2}})=({{x}_{1}}+{{x}_{2}})+i({{y}_{1}}+{{y}_{2}}) \\
& \Rightarrow ({{x}_{1}}+i{{y}_{1}})+({{x}_{2}}+i{{y}_{2}}) \\
& \Rightarrow {{z}_{1}}+{{z}_{2}} \\
\end{align}$
Thus, the point ${{P}_{3}}$ is represented by ${{z}_{1}}+{{z}_{2}}$.
Option ‘A’ is correct
Note: Here we need to remember that, the required point is one of the vertices of the given parallelogram. So, the property of the parallelogram is applied to find the required vertex.
Recently Updated Pages
JEE Advanced 2026 Revision Notes for Vectors - Free PDF Download

JEE Advanced 2026 Revision Notes for Trigonometry - Free PDF Download

JEE Advanced 2026 Surface Chemistry Revision Notes - Free PDF Download

JEE Advanced Study Plan 2026: Expert Tips and Preparation Guide

JEE Advanced 2026 Revision Notes for Chemistry Solutions - Free PDF Download

Solutions Class 12 Notes JEE Advanced Chemistry [PDF]

Trending doubts
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

Difference Between Exothermic and Endothermic Reactions Explained

IIT CSE Cutoff: Category‐Wise Opening and Closing Ranks

IIT Fees Structure 2025

Top IIT Colleges in India 2025

Other Pages
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

NCERT Solutions For Class 11 Maths Chapter 12 Limits and Derivatives (2025-26)




