JEE Advanced 2023 Revision Notes for Trigonometry

Trigonometry:

Trigonometry deals with measuring the angles and sides of a triangle. Usually, trigonometry is considered for the right-angled triangle. Also, its functions are used to find out the length of the arc of a circle, which forms a section in the circle with a radius and its centre point.

Trigonometry Formulas:

Starting with the basics of trigonometry formula, for a right-angled triangle ABC perpendicular at B, having an angle θ, opposite to perpendicular (AB), we can define trigonometric ratios as;

$\operatorname{Sin} \theta  = \dfrac{P}{H}$ 

$\operatorname{Cos} \theta  = \dfrac{B}{H}$

$\operatorname{Tan} \theta  = \dfrac{P}{B}$

$Cot\theta  = \dfrac{B}{P}$

$\operatorname{Sec} \theta  = \dfrac{H}{B}$

$\operatorname{csc} \theta  = \dfrac{H}{P}$

Where,

P= perpendicular

B=base

H=hypotenuse 

Trigonometry Functions:

Trigonometry functions are measured in terms of radian for a circle drawn in the XY plane. Radian is nothing but the measure of an angle, just like a degree. The difference between the degree and radian is

Degree: If rotation from the initial side to the terminal side is ${\left( {\dfrac{1}{{360}}} \right)^{th}}$ of revolution, then the angle is said to measure 1 degree.

1 degree = 60minutes

1 minute = 60 seconds

Radian: If an angle is subtended at the center by an arc of length ‘l, the angle is measured as radian. Suppose $\theta$ is the angle formed at the center, then

$\theta$ =Length of the arc/radius of the circle.

$\theta$ =l/r

Relation Between Degree and Radian:

$2\pi$  radian = ${360^0}$ 

Or

$\pi$  radian = ${180^0}$ 

Where $\pi$ =22/7

The above relationship allows us to formulate a radian measure in degree measure and a degree measure in radian measure. We know that the approximate value of pi ($\pi $) is 22/7. By substituting this value in the above relation, we get

1 radian = ${180^0}$ / $\pi $ = ${57^0}16'$ 

Also,

${1^0} = \pi /80$ radian = 0.01746 radian.

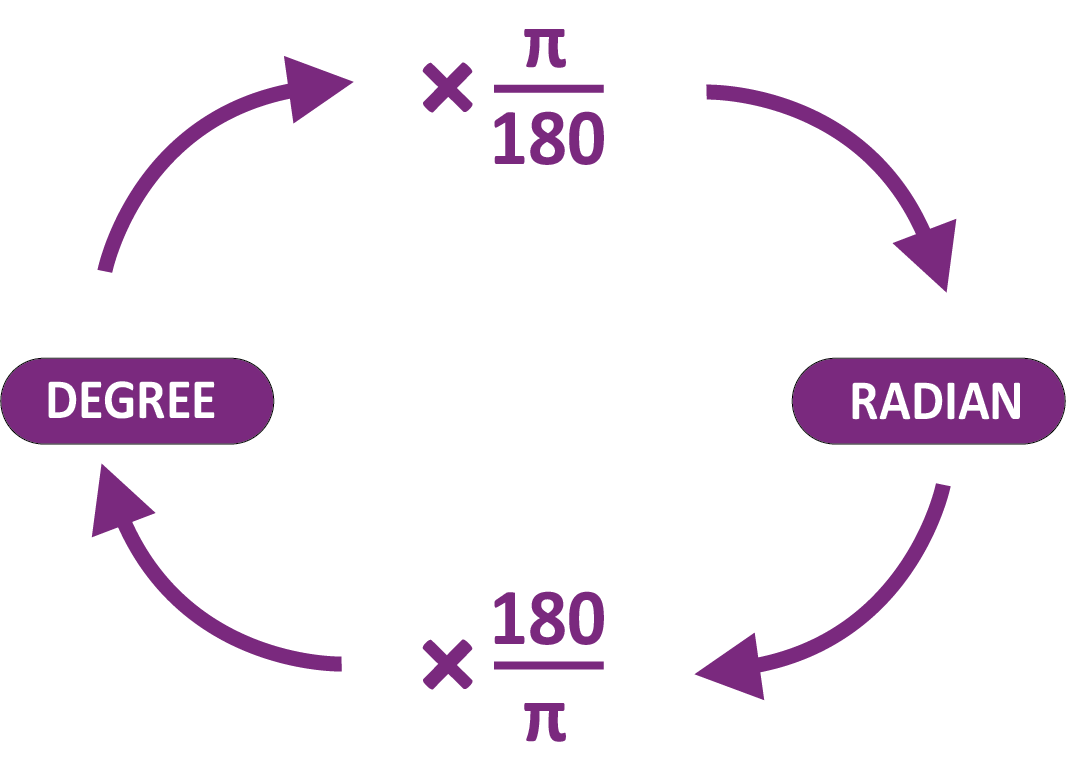
Convert

The relation between degree measures and radian measures of some standard angles can be observed.

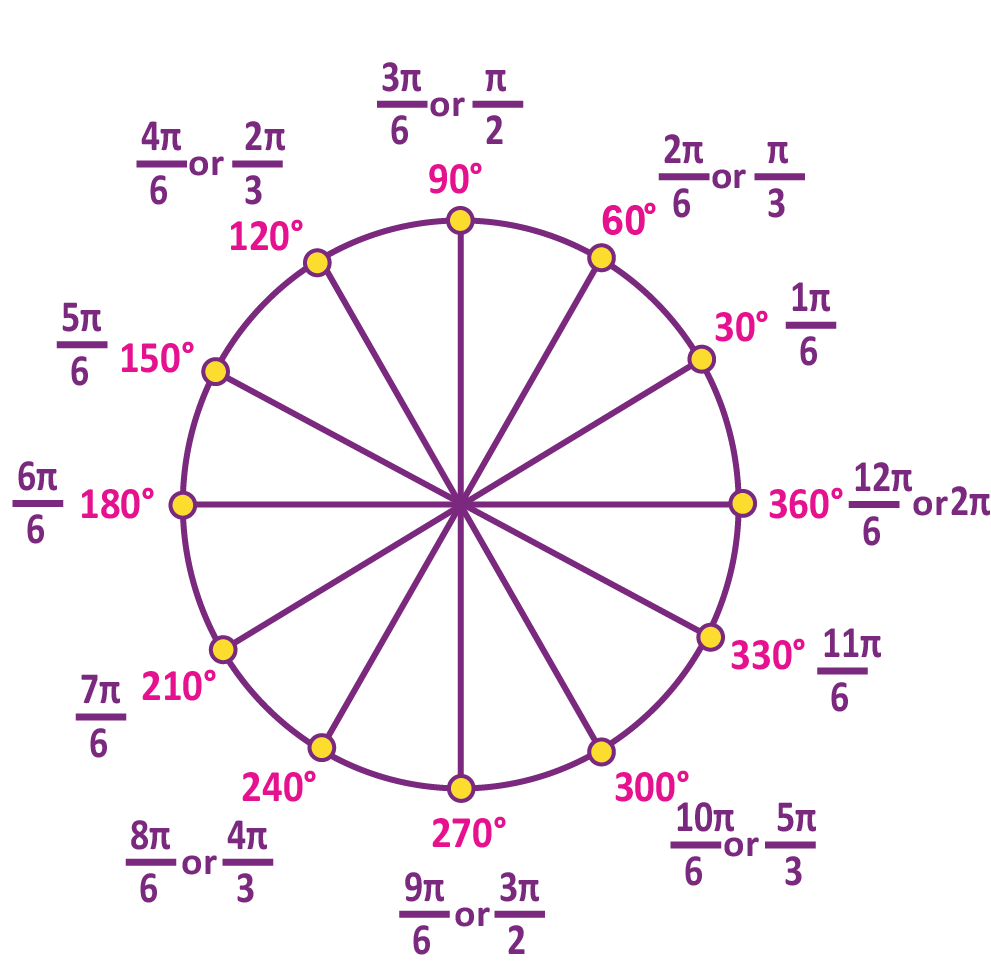
Relation Between Degree and Radian

Example 1: Convert 135 degrees to radians.

Solution:

135⁰ = 135⁰ x (π/180⁰)

= 3π/4 rad

Or

= 2.355 rad (approx)

Table for Degree and Radian Relation:

Trigonometry Table:

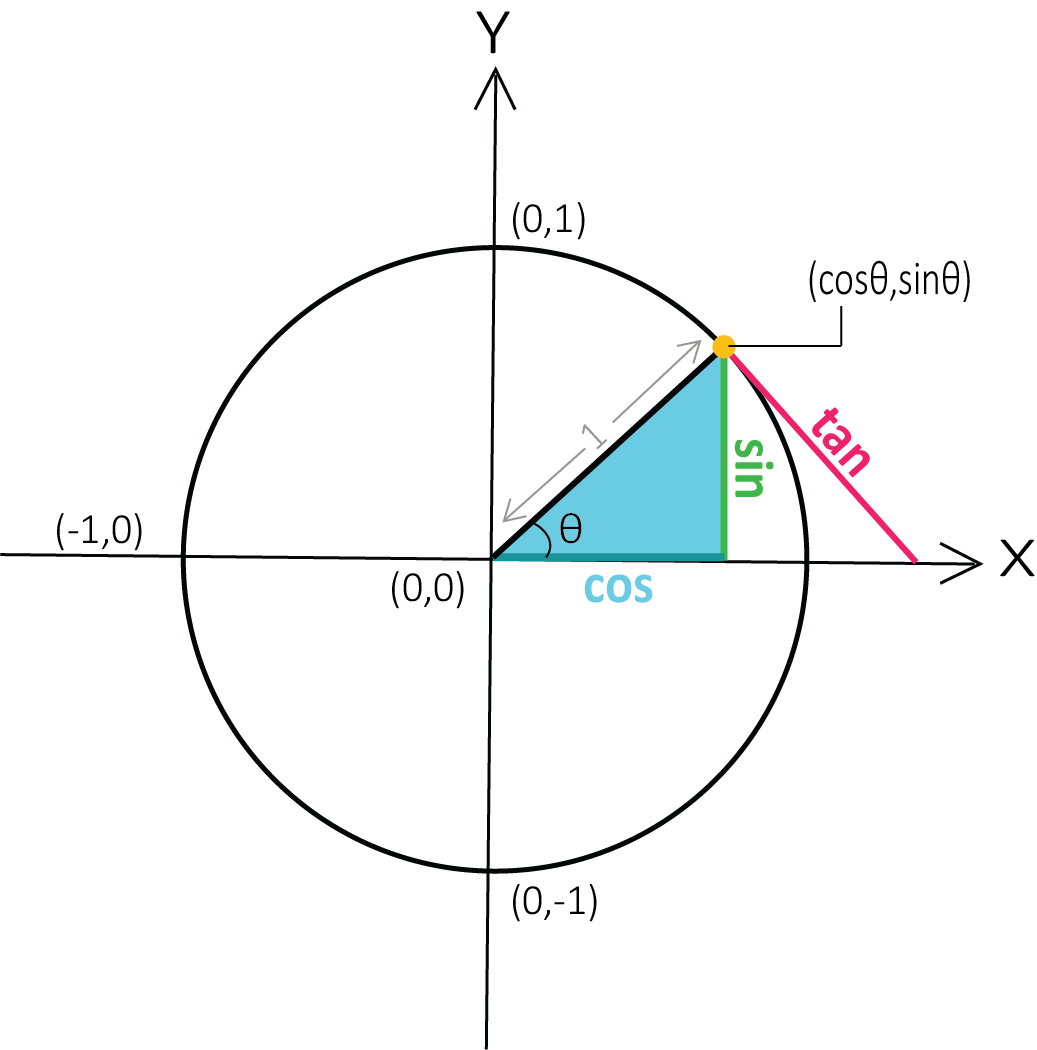
Trigonometric Signs

Sign of Trigonometry Functions:

$(\operatorname{Cos} {( - }\theta ) = \operatorname{Cos} \theta$

$\operatorname{Sin} {(- }\theta ){ = - }\operatorname{Sin} \theta$ 

$\operatorname{Tan} {(- }\theta ){ = - }Tan~\theta$ 

$Cot{(^ - }\theta ){ = - }Cot~\theta$ 

$\operatorname{Sec} {(- }\theta ) = \operatorname{Sec} \theta$ 

$\operatorname{csc} {( - }\theta ){ =  - }\operatorname{csc}\theta$

In trigonometry, there are six functions, namely sin, cos, tan, csc, sec and tan. We can determine the sign of the trigonometric function with the help of a unit circle. Let P(a, b) be a point on the unit circle with the centre at the origin.

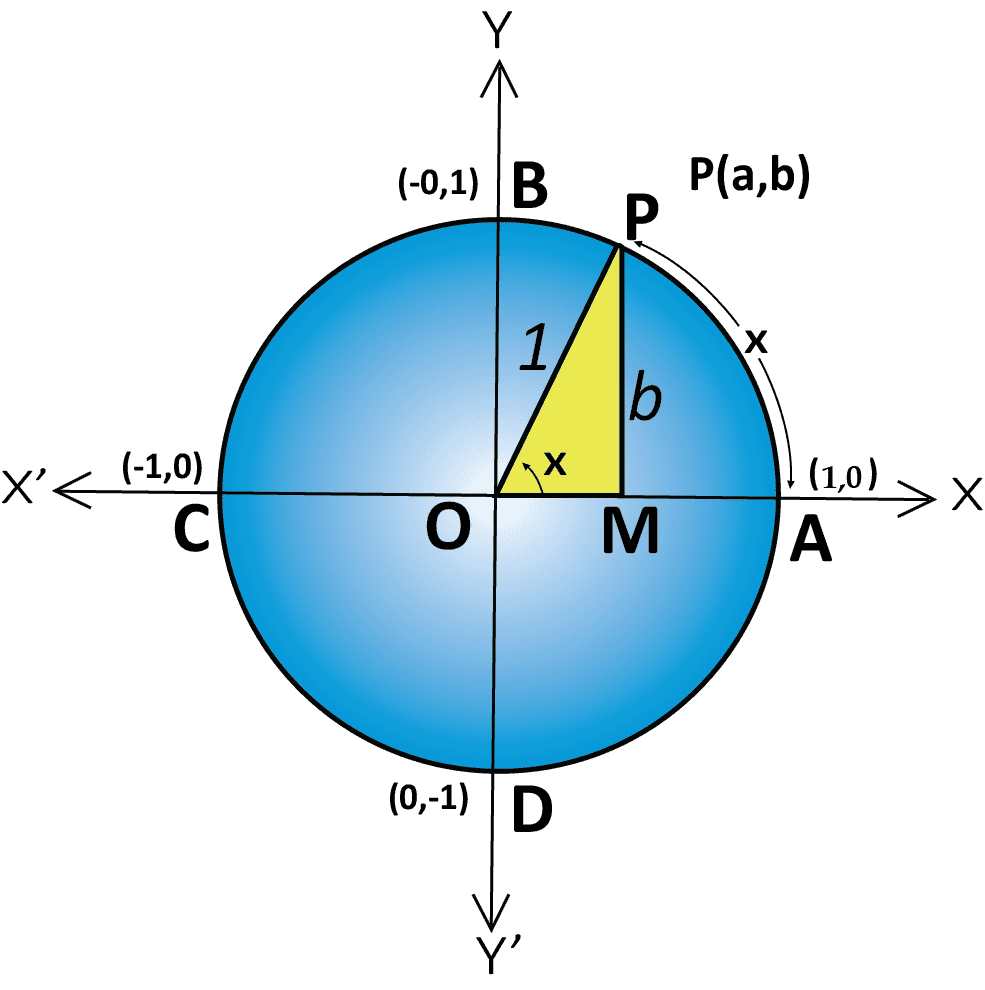
Function of Trigonometry

For every point P (a, b) on the unit circle, – 1 ≤ a ≤ 1 and – 1 ≤ b ≤ 1, we have – 1 ≤ cos x ≤ 1 and –1 ≤ sin x ≤ 1 for all x. Also, we can define the values of a and b in different quadrants as

The first quadrant: 0 < x < π/2 ⇒ a and b are positive

Second quadrant: π/2 < x < π ⇒ a is negative and b is positive

Third quadrant: π < x < 3π/2 ⇒ a and b are negative

Fourth quadrant: 3π/2 < x < 2π ⇒ a is positive and b is negative.

The Sign of Trigonometric Functions in Each Quadrant

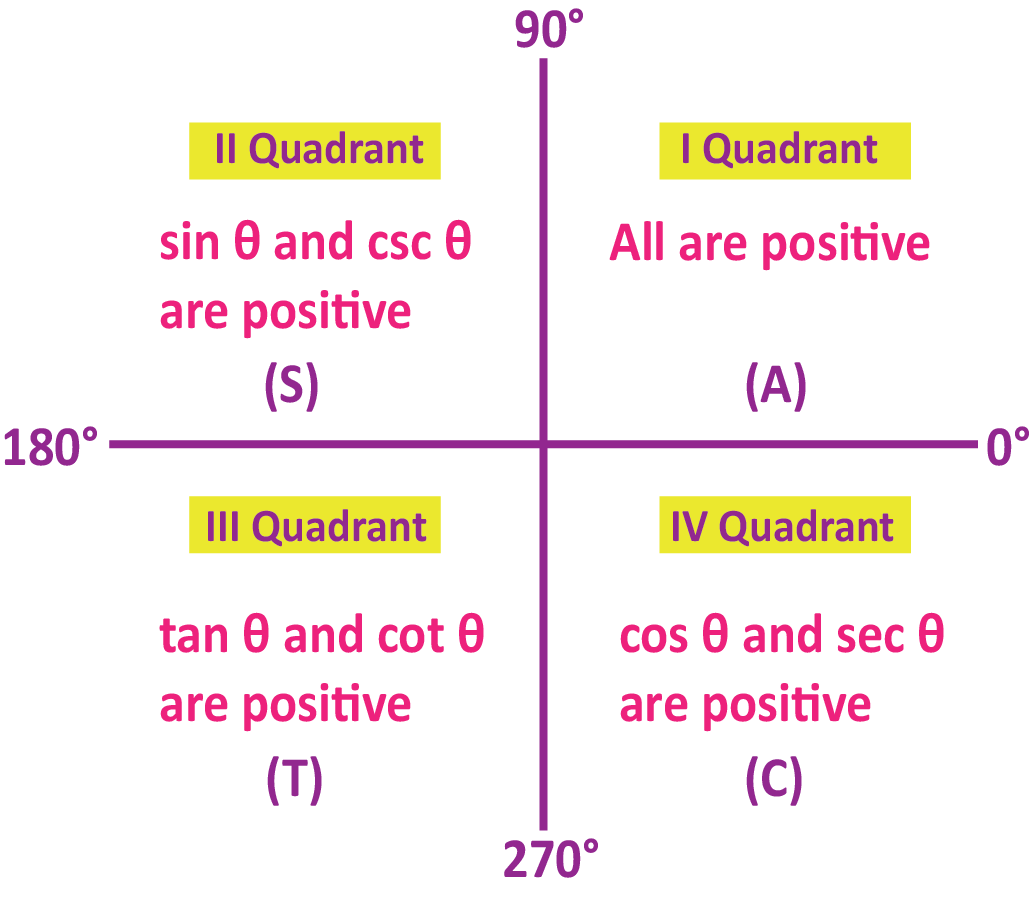
Quadrant

In the first quadrant, all functions are positive, in the 2nd quadrant, only sin and csc are positive, in the 3rd quadrant only tan and cot are positive, whereas in the 4th quadrant only cos and sec are positive. Thus, we can tabulate the signs of different trigonometric functions in different quadrants as follows:

Also, go through the table given below to understand the behaviour of trigonometric functions with respect to their values in different quadrants.

Graphs of Trigonometry Functions:

The trigonometric functions are:

1. Sine

2. Cosine

3. Tangent

4. cosec

5. Secant

6. Cotangent

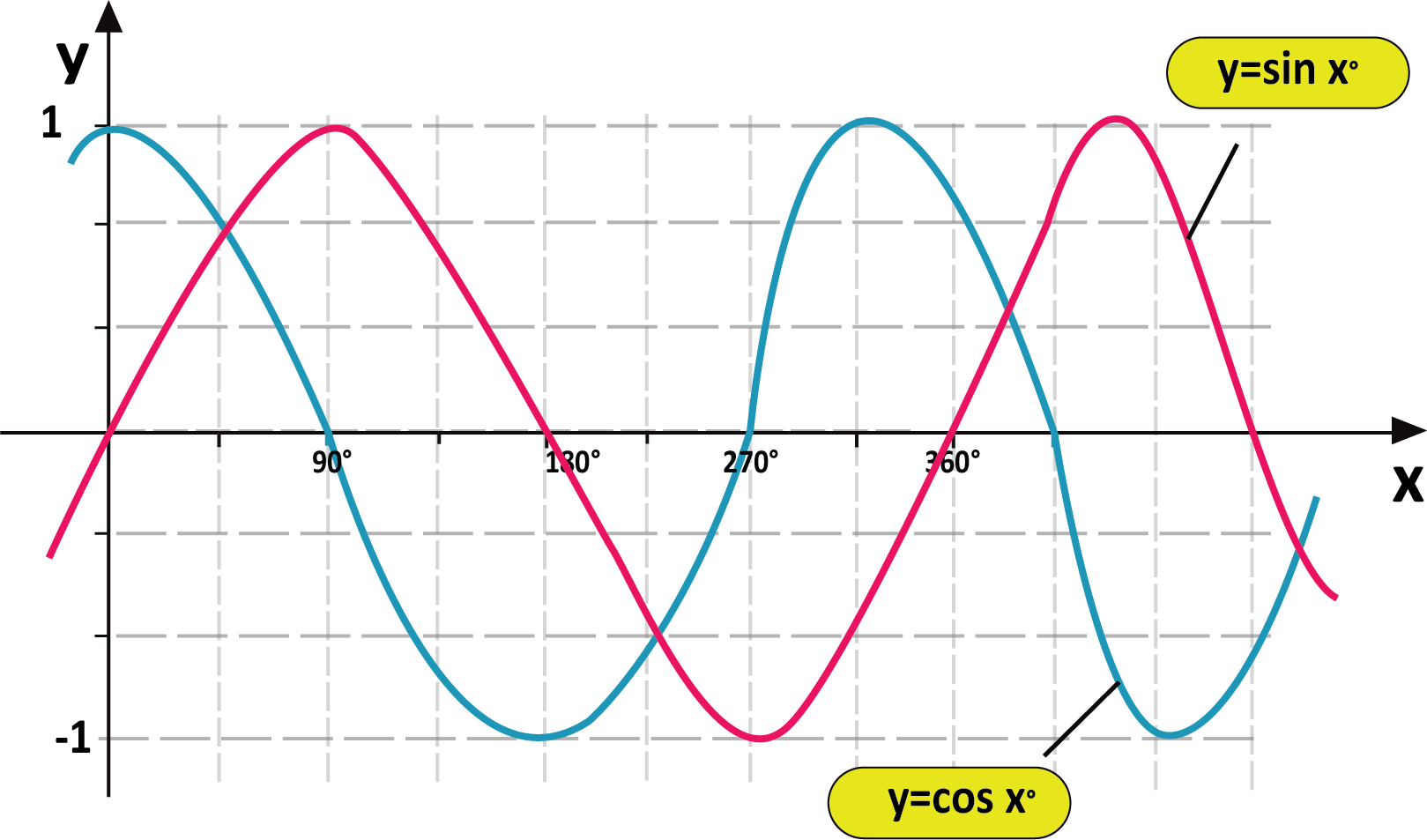
Sine, Cosine and tangent are the three important trigonometry ratios, based on which functions are defined. Below are the graphs of the three trigonometry functions sin x, cos x, and tan x. In these trigonometry graphs, x-axis values of the angles are in radians, and on the y-axis, its f(x) is taken, the value of the function at each given angle.

Sin Graph:

• $Y = \sin x$

• The roots or zeros of $Y = \sin x$ is at the multiples of π

• The sin graph passes the x-axis as sin x = 0 there

• Period of the sine function is 2π

• The height of the curve at each point is equal to the line value of sine
  
  

Cos Graph:

• $Y = \cos x$

• $\sin \left( {x + \dfrac{\pi }{2}} \right)$ = cos x

• y = cos x graph is the graph we get after shifting $Y = \sin x$ to  π/2 units to the left

• Period of the cosine function is 2π
  
  

There are a few similarities between the sine and cosine graphs, They are:

1. Both have the same curve which is shifted along the x-axis

2. Both have an amplitude of 1

3. Have a period of 360° or 2π radians

The combined graph of sine and cosine function can be represented as follows.

Tan Graph

Example: If $\cot x =  - \dfrac{5}{{12}}$, x lies in the fourth quadrant, then find the value of csc x.

Solution: Given, $\cot x =  - \dfrac{5}{{12}}$

We know that,

$\csc{^2}x - {\cot ^2}x = 1$

$\csc{^2}x = 1 + {\cot ^2}x$

= $1 + {\left( {\dfrac{{ - 5}}{{12}}} \right)^2}$

= $1 + \left( {\dfrac{{25}}{{144}}} \right)$

= $1 + \dfrac{{\left( {144 + 25} \right)}}{{144}}$

= $\dfrac{{169}}{{144}}$

$\csc~x = \sqrt {\left( {\dfrac{{169}}{{144}}} \right)}  =  \pm \dfrac{{13}}{{12}}$

Given that x lies in the fourth quadrant and csc x is negative in the fourth quadrant.

Therefore, $\csc~x =  - \dfrac{{13}}{{12}}$

Similarly, we can solve various types of trigonometry problems quickly. These are useful in determining the values of trigonometry functions which are dependent on other functions and trigonometry angles also.

Example: What will be the value of $\sec ^{-1}\left(\dfrac{1}{4} \sum_{k=0}^{10} \sec \left(\dfrac{7 \pi}{12}+\dfrac{k \pi}{2}\right) \sec \left(\dfrac{7 \pi}{12}+\dfrac{(k+1) \pi}{2}\right)\right)$ in the interval $\left[-\dfrac{\pi}{4}, \dfrac{3 \pi}{4}\right]$ equals to _________.

Answer: 0

Explanation

$\sec ^{-1}\left(\dfrac{1}{4} \sum_{k=0}^{10} \sec \left(\dfrac{7 \pi}{12}+\dfrac{k \pi}{2}\right) \sec \left(\dfrac{7 \pi}{12}+\dfrac{(k+1) \pi}{2}\right)\right)$

$=\sec ^{-1}\left(-\dfrac{1}{4} \sum_{k=0}^{10} \sec \left(\dfrac{7 \pi}{12}+\dfrac{k \pi}{2}\right) \operatorname{csc}\left(\dfrac{7 \pi}{12}+\dfrac{k \pi}{2}\right)\right)$

$=\sec ^{-1}\left(-\dfrac{1}{2} \sum_{k=0}^{10} \dfrac{1}{\sin \left(\dfrac{7 \pi}{6}\right) \cdot(-1)^{k}}\right)$

$=\sec ^{-1}\left(-\dfrac{1}{2} \dfrac{1}{\sin \left(\dfrac{7 \pi}{6}\right)}\right)$

$=\sec ^{-1}(1)=0$

Importance of Trigonometry

Trigonometric ratios are determined by measuring the length of different sides of a right-angled triangle. On proceeding further, the relationships between two trigonometric ratios can also be identified using various formulas.

These relationships become universal for all kinds of angles existing in a right-angled triangle. Hence, these relationships are then termed identities. They will remain the same and can be used for solving sums based on trigonometry.

The trigonometric functions are covered in this chapter along with some changes in values and signs. Learn how these functions are applied to different cases. This chapter is of utmost importance as the knowledge of trigonometric functions will be required in different fields as well.

This chapter helps students lay a strong foundation for the values of trigonometric ratios of various angles. These revision notes will help them determine the implications of such functions and identities easily.

Benefits of Trigonometry JEE Advanced Revision Notes

• These revision notes have been prepared by the top teachers of Vedantu providing an easier explanation of all the identities and formulas covered in this chapter. The basic concept of formulating a trigonometric identity or a function will become much clearer to you with the help of these notes.

• Use these notes to prepare and revise this chapter before the exams. There is no need to make notes by yourself when you can avail of these expert-prepared notes for free. 

• Refer to these revision notes to solve and practice the trigonometric identities and functions at your convenience and to study this chapter efficiently.

• Solve and practice the sums of this chapter with the help of these revision notes to evaluate your understanding. Thus, you can find out the areas in which you need to work harder and complete your Trigonometry JEE Advanced revision before the exam.

Download Trigonometry JEE Advanced Notes PDF for Free

You can download these revision notes in PDF format and make a quick review of the concepts covered in this chapter. Going through these notes will help you to remember all you have studied in this chapter. Find out how the experts have solved sample questions and learn the techniques to determine the right answers from these revision notes. Trigonometry can be a little tricky as the same identities have multiple applications. So refer to this Trigonometry JEE Advanced Notes PDF for your exam preparation and score well in the exam.

Important Related Links for JEE Main and JEE Advanced