Question

If the height of the tower and the distance of the point of observation from its foot both are increased by 10%, then the angle of elevation remains unchanged.

Answer 1

Hint: We use the formula of tan of an angle in the right angle triangle and write the fraction in terms of initial length of tower and distance of foot of tower and point of observation. Using the method of percentage we find the new lengths and again apply tan of angle but with new angle of elevation.
* We can write \[m\% \] of \[x\]as\[\dfrac{m}{{100}}x\].
* In a right angled triangle, tan of an angle is given by dividing perpendicular of triangle by base of triangle.

Complete step-by-step answer:
We draw a triangle ABC where AB is the height of the tower and BC is the distance of the foot of tower from point of observation.
 

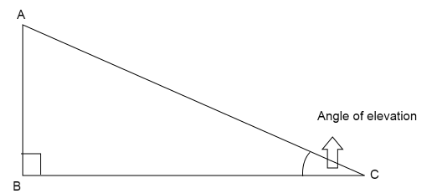
Let us assume the angle of elevation\[\angle BCA = \theta \].
Since the tower is perpendicular to the ground, then we can say triangle ABC is a right angled triangle.
Now we know \[\tan \theta = \]Perpendicular divided by base.
\[ \Rightarrow \tan \theta = \dfrac{{AB}}{{BC}}\] … (1)
Now we increase the lengths AB and BC both by 10% each

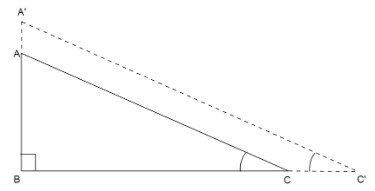
We find the lengths A’B and BC’
We have\[A'B = AB + 10\% AB\]
We can write percentage in fraction form as
\[ \Rightarrow A'B = AB + \dfrac{{10}}{{100}}AB\]
Take AB common in RHS
\[ \Rightarrow A'B = AB\left( {1 + \dfrac{{10}}{{100}}} \right)\]
Take LCM inside the bracket
\[ \Rightarrow A'B = AB \times \dfrac{{110}}{{100}}\]
Cancel the same terms from numerator and denominator.
\[ \Rightarrow A'B = \dfrac{{11}}{{10}}AB\] … (2)
Now we have \[BC' = BC + 10\% BC\]
We can write percentage in fraction form as
\[ \Rightarrow BC' = BC + \dfrac{{10}}{{100}}BC\]
Take BC common in RHS
\[ \Rightarrow BC' = BC\left( {1 + \dfrac{{10}}{{100}}} \right)\]
Take LCM inside the bracket
\[ \Rightarrow BC' = BC \times \dfrac{{110}}{{100}}\]
Cancel the same terms from numerator and denominator.
\[ \Rightarrow BC' = \dfrac{{11}}{{10}}BC\] … (3)
Now for the new angle of elevation after the increase of height and the distance from foot
Let \[\angle BC'A' = \phi \]
Then in right angle triangle A’BC’
\[\tan \phi = \dfrac{{A'B}}{{BC'}}\]
Substitute the values in numerator and denominator from equations (3) and (4)
\[ \Rightarrow \tan \phi = \dfrac{{\dfrac{{11}}{{10}}AB}}{{\dfrac{{11}}{{10}}BC}}\]
Cancel same fractions in numerator and denominator
\[ \Rightarrow \tan \phi = \dfrac{{AB}}{{BC}}\]
Substitute the value of fraction in RHS from equation (1)
\[ \Rightarrow \tan \phi = \tan \theta \]
Take inverse tan function on both sides of the equation.
\[ \Rightarrow {\tan ^{ - 1}}(\tan \phi ) = {\tan ^{ - 1}}(\tan \theta )\]
Cancel inverse and the function with each other on both sides of the equation.
\[ \Rightarrow \theta = \phi \]

So, the angle of elevation remains unchanged.

Note: Students might try to solve this by applying Pythagoras theorem but that will only give us the change in hypotenuse. Also, keep in mind to associate the percentage with the same side when calculating the change in length of side, many students just write 10% and don’t multiply with the side.