
If ${S_1}$ and ${S_2}$ are two hollow spheres enclosing charges $q$ and $2q$ respectively then what is the ratio of electric flux through ${S_1}$ and ${S_2}$? How will the electric flux through ${S_1}$ change if a medium of di-electric constant $5$ is introduced inside ${S_1}$.

Answer
551.4k+ views
Hint: we will first calculate the electric flux by using the Gauss’ law. After this, we will find the ratio of the electric flux by dividing both the electric flux. Now, the change in the electric flux can be calculated by using the potential difference formula.
Formula used:
The formula of potential difference is given by
$V = Ed$
Here, $V$ is the potential difference, $E$ is the electric field and $d$ is the distance between the plates.
Complete step by step answer:
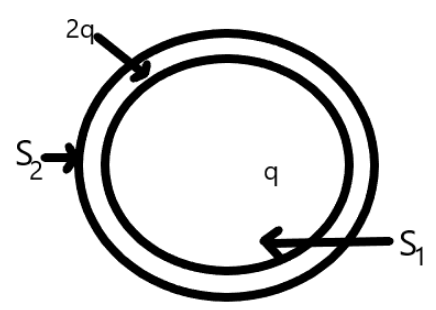
Consider two hollow spheres ${S_1}$ and ${S_2}$ that will enclose charges $$q$$ and $2q$ respectively as shown below;
Now, let the electric flux enclosed by the sphere ${S_1}$ is ${\phi _1}$ and the electric flux enclosed by the sphere ${S_2}$ is ${\phi _2}$.Now, from the Gauss’ law, the electric flux is given by,
$\phi = \dfrac{q}{{{\varepsilon _0}}}$
Therefore, the electric flux in the sphere ${S_1}$ is given by
${\phi _1} = \dfrac{q}{{{\varepsilon _0}}}$
Also, the electric flux in the sphere ${S_2}$ is given by
${\phi _2} = \dfrac{{3q}}{{{\varepsilon _0}}}$
Now, the ratio of the electric flux is given below
$\dfrac{{{\phi _1}}}{{{\phi _2}}} = \dfrac{1}{3}$
Now, according to coulomb’s law of charges, the potential difference between the charges is given by
$V = Ed$
Here, $E$ is the electric field in the sphere and is given by
$E = \dfrac{q}{{A{\varepsilon _0}}}$
Therefore, the value of potential difference is given by
$V = \dfrac{q}{{A{\varepsilon _0}}}d$
$ \Rightarrow \,V = \phi \dfrac{d}{A}$
$ \therefore \,\phi = \dfrac{{AV}}{d}$
Therefore, from the above equation, we can say that the flux $\phi $ in the sphere will be inversely proportional to distance $d$.Now, if the di-electric of $5$ is introduced inside the sphere ${S_1}$ , the distance $d$ will increase by $5$ times and therefore, the electric flux will increase by $\dfrac{1}{5}$ times.
Note:Now, you might get confused about how the charge of the sphere ${S_2}$ is $3q$. This is because the sphere ${S_2}$ contains the sphere ${S_1}$, therefore, the charge will add up. Also, we have used the concept of capacitors that contains two capacitors.
Formula used:
The formula of potential difference is given by
$V = Ed$
Here, $V$ is the potential difference, $E$ is the electric field and $d$ is the distance between the plates.
Complete step by step answer:
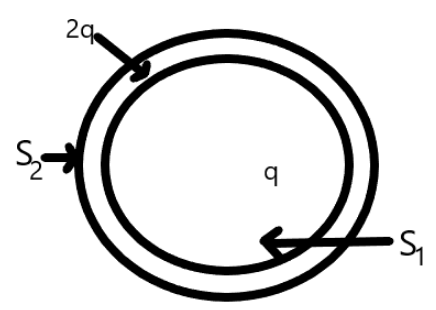
Consider two hollow spheres ${S_1}$ and ${S_2}$ that will enclose charges $$q$$ and $2q$ respectively as shown below;

Now, let the electric flux enclosed by the sphere ${S_1}$ is ${\phi _1}$ and the electric flux enclosed by the sphere ${S_2}$ is ${\phi _2}$.Now, from the Gauss’ law, the electric flux is given by,
$\phi = \dfrac{q}{{{\varepsilon _0}}}$
Therefore, the electric flux in the sphere ${S_1}$ is given by
${\phi _1} = \dfrac{q}{{{\varepsilon _0}}}$
Also, the electric flux in the sphere ${S_2}$ is given by
${\phi _2} = \dfrac{{3q}}{{{\varepsilon _0}}}$
Now, the ratio of the electric flux is given below
$\dfrac{{{\phi _1}}}{{{\phi _2}}} = \dfrac{1}{3}$
Now, according to coulomb’s law of charges, the potential difference between the charges is given by
$V = Ed$
Here, $E$ is the electric field in the sphere and is given by
$E = \dfrac{q}{{A{\varepsilon _0}}}$
Therefore, the value of potential difference is given by
$V = \dfrac{q}{{A{\varepsilon _0}}}d$
$ \Rightarrow \,V = \phi \dfrac{d}{A}$
$ \therefore \,\phi = \dfrac{{AV}}{d}$
Therefore, from the above equation, we can say that the flux $\phi $ in the sphere will be inversely proportional to distance $d$.Now, if the di-electric of $5$ is introduced inside the sphere ${S_1}$ , the distance $d$ will increase by $5$ times and therefore, the electric flux will increase by $\dfrac{1}{5}$ times.
Note:Now, you might get confused about how the charge of the sphere ${S_2}$ is $3q$. This is because the sphere ${S_2}$ contains the sphere ${S_1}$, therefore, the charge will add up. Also, we have used the concept of capacitors that contains two capacitors.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Differentiate between action potential and resting class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




