Question

If O is vertex of parabola and the foot of perpendicular be H from the focus S on any tangent to a parabola at any point P, then OS, OH, SP are in
(A). A.P
(B). G.P
(C). H.P
(D). A.G.P

Answer 1

Hint: Here we first calculate the coordinates of each point and get the distance OH, OS, SP. After that we need to check the condition which one is satisfying from the option.

Complete step-by-step answer:
Let’s assume parabola ${y^2} = 4ax$
We know that parametric coordinates of any point on parabola is $\left( {a{t^2},2at} \right)$ where t is a parameter

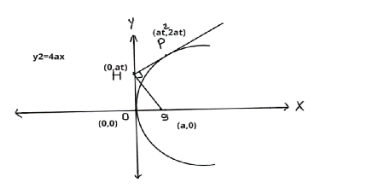
Now we can write the equation of tangent at point (P)
$ty = x + a{t^2}$

To determine the coordinate of point H, put the value of x as zero.
Therefore, the coordinate of point H is (0, at)

Now we calculate the distance between two points S and H
$SH = \sqrt {{{\left( {0 - a} \right)}^2} + {{\left( {at - 0} \right)}^2}} = \sqrt {{a^2} + {a^2}{t^2}} $

Similarly, we calculate the distance between two points O and S
$OS = \sqrt {{{\left( {0 - a} \right)}^2} + {{\left( {0 - 0} \right)}^2}} = \sqrt {{a^2}} = 0$

Similarly, we calculate the distance between two points S and P
$SP = \sqrt {{{\left( {a{t^2} - a} \right)}^2} + {{\left( {2at - 0} \right)}^2}} = a\left( {1 + {t^2}} \right)$
Now we clearly see that
$S{H^2} = OS \cdot SP$
This is the condition of G.P
So, option (b) is correct.

NOTE:
Any point on parabola ${y^2} = 4ax$ is $\left( {a{t^2},2at} \right)$ and we refer to it as the point ‘t’. Here, ‘t’ is a parameter i.e. it varies from point to point.