Question

If B is a $3 \times 3$ matrix such that ${B^2} = 0$ then $\det [{(I + B)^{50}} - 50B]$ is equal to:-
A) 1
B) 3
C) 24
D) 50

Answer 1

Hint: Here in this question some matrix properties, binomial expansion and combination formula will get used which are mentioned below:-
Combination formula:- $^n{C_r} = \dfrac{{n!}}{{r!(n - r)!}}$
${\left( I \right)^n} = \left( I \right)$
$\left( A \right)\left( I \right) = \left( A \right)$
${(x + y)^n} = \sum\limits_{k = 0}^n {^n{C_k}.{x^k}{y^{n - k}} = {[^n}{C_0}{x^n}{y^0}{ + ^n}{C_1}{x^{n - 1}}{y^1}{ + ^n}{C_2}{x^{n - 2}}{y^2}......{ + ^n}{C_n}{x^0}{y^n}} $

Complete step-by-step answer:
B is a $3 \times 3$ matrix such that ${B^2} = 0$ so if we multiply B matrix on both sides then we will get higher power B values.
 $ \Rightarrow \left( B \right){\left( B \right)^2} = \left( B \right)0$
$ \Rightarrow {\left( B \right)^3} = 0$
Similarly if we multiply $\left( B \right)$ again then we will get
$ \Rightarrow \left( B \right){\left( B \right)^3} = \left( B \right)0$
$ \Rightarrow {\left( B \right)^4} = 0$
So we can conclude that ${\left( B \right)^n} = 0$ for $n \ge 2$
Now we will apply binomial expansion inside the given matrix $\det [{(I + B)^{50}} - 50B]$
$ \Rightarrow {(I + B)^{50}}{ = ^{50}}{C_0}.{I^{50}}{ + ^{50}}{C_1}.{I^{49}}.B{ + ^{50}}{C_2}.{I^{48}}.{B^2}.......{ + ^{50}}{C_{50}}.{B^{50}}$
As we have proved above, ${\left( B \right)^n} = 0$ for $n \ge 2$ so all matrices B with having power higher than equal to 2 will become zero.
 $ \Rightarrow {(I + B)^{50}}{ = ^{50}}{C_0}.{I^{50}}{ + ^{50}}{C_1}.{I^{49}}.B$
Now we know that identity matrix multiplied n times gives an identity matrix so we will use this property.
 $ \Rightarrow {(I + B)^{50}}{ = ^{50}}{C_0}.I{ + ^{50}}{C_1}.I.B$
Now we will apply combination formula $^n{C_r} = \dfrac{{n!}}{{r!(n - r)!}} = \dfrac{{50!}}{{0!(50 - 0)!}} = 1$
$^n{C_r} = \dfrac{{n!}}{{r!(n - r)!}} = \dfrac{{50!}}{{1!(50 - 1)!}} = \dfrac{{50 \times 49!}}{{49!}} = 50$
$ \Rightarrow {(I + B)^{50}} = I + 50I.B$
Using identity $\left( A \right)\left( I \right) = \left( A \right)$we will get,
$ \Rightarrow {(I + B)^{50}} = I + 50B$
Now we will put this value in the main equation given in question.
$ \Rightarrow \det [I + 50B - 50B]$
Now we will cancel equal and opposite in sign terms.
$ \Rightarrow \det [I]$ And determinant of identity matrix is 1
$\therefore \det [{(I + B)^{50}} - 50B] = 1$
Therefore correct option is (A).

Note: Sometimes it is really very confusing to find determinant, so just be patient and only follow some simple rules. Always start from the left side of the matrix and pick the top element then multiply that element to the lower element of the right side then put minus sign and then take top element of right side and multiply it with lower element of left side. It’s just like crisscross. To understand more neatly below is the diagram.

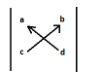
Determinant will be |ad-cb|