Question

If \[A\subset B,n\left( A \right)=5\] and \[n\left( B \right)=7\], then \[n\left( A\cup B \right)=\]_ _ _ _ _ _ _ _ _.
(a) 5
(b) 7
(c) 2
(d) 12

Answer 1

Hint: Use the formula for union of two sets that is \[n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)\]. Now, since \[A\subset B\], therefore put \[n\left( A\cap B \right)=n\left( A \right)\], then use the given information that is \[n\left( A \right)=5\] and \[n\left( B \right)=7\].

Here, we are given two sets A and B such that \[A\subset B\], \[n\left( A \right)=5\] and \[n\left( B \right)=7\]. We have to find the value of \[n\left( A\cup B \right)\].
Before proceeding with the question, we must know some of the terminologies related to sets.
First of all, a ‘set’ is a collection of well-defined and distinct objects. The most basic property of a set is that it has elements. The number of elements of a set, say A is shown by \[n\left( A \right)\].
Here, in the question we have \[n\left( A \right)=5\] and \[n\left( B \right)=7\], that means the number of elements in set A is 5, while the number of elements in set B is 7.
Now, a ‘subset’ is a set which is contained in another set. We can also put it as, if we have a set P which is a subset of another set Q, then P is contained in Q as all the elements of set P are elements of Q. This relationship is shown by \[P\subset Q\].
We can show it diagrammatically as,

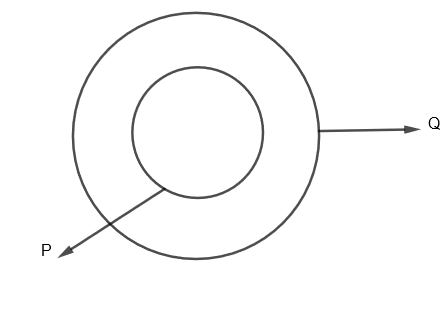
Here, \[P\subset Q\], that means P is contained in Q as P is a subset of Q.
In question, we are given that \[A\subset B\], that means that A is a subset of B or A is contained in B. We can show them as

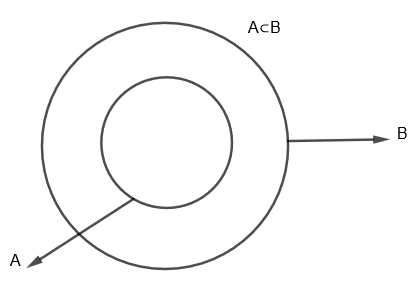
Now, union of two sets say P and Q is the set of elements which are in P, in Q or both P and Q. For example, if P = {1, 3, 5, 7} and Q = {1, 2, 4, 6, 7}, then union of P and Q which is shown as \[P\cup Q=\left\{ 1,2,3,4,5,6,7 \right\}\]
Diagrammatically, the shaded portion is \[P\cup Q\] which is as follows

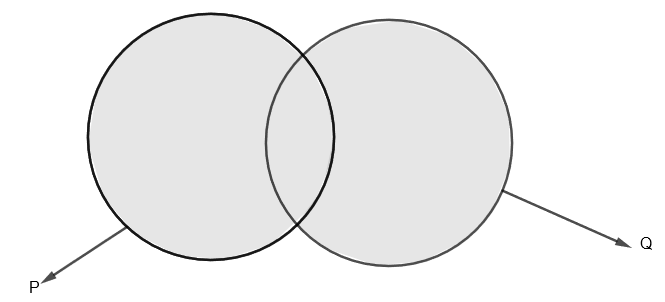
The formula for \[n\left( P\cup Q \right)=n\left( P \right)+n\left( Q \right)-n\left( P\cap Q \right)\].
Here, \[P\cap Q\] is the area common to both P and Q.
Now, in the given question, we have to find \[n\left( A\cup B \right)\], that is, the number of elements in A union B.
We can show \[A\cup B\] by a shaded portion which is as follows.

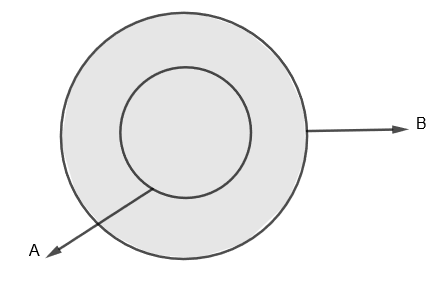
Here, \[A\subset B\] and \[n\left( A \right)=5\] and \[n\left( B \right)=7\].
Here, we can see that the portion common to the set A and B that is \[\left( A\cap B \right)\] is nothing but set A. Therefore, here we have \[n\left( A\cap B \right)=n\left( A \right)=5\].
As we know that \[n\left( P\cup Q \right)=n\left( P \right)+n\left( Q \right)-n\left( P\cap Q \right)\], therefore to get \[n\left( A\cup B \right)\], we will put A and B in place of P and Q respectively, we will get
\[n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)\]
Since, we have found that \[n\left( A\cap B \right)=n\left( A \right)=5\].
Therefore we get, \[n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)-n\left( A \right)\]
By putting the values of n (A) and n (B), we get,
\[n\left( A\cup B \right)=5+7-5\]
\[n\left( A\cup B \right)=7\]
Therefore, we get \[n\left( A\cup B \right)=7\]
Hence, option (b) is correct.

Note: Students must note that whenever \[A\subset B\], that is A is subset of B, then \[n\left( A\cup B \right)\], that is the number of elements in A union B is equal to number of elements in set B that is, \[n\left( A\cup B \right)=n\left( B \right)\] when \[A\subset B\]. Also, some students make this mistake of writing \[n\left( A\cup B \right)=n\left( A \right)+n\left( B \right)\] which is wrong. They must remember to subtract \[n\left( A\cap B \right)\] as well. Hence, \[n\left( A\cap B \right)=n\left( A \right)+n\left( B \right)-n\left( A\cap B \right)\].