Question

If an isosceles triangle of vertical angle $2\theta $ is inscribed in a circle of radius $a$. Then, area of the triangle is maximum, when $\theta $ is equal to
A. $\dfrac{\pi }{6}$
B. $\dfrac{\pi }{4}$
C. $\dfrac{\pi }{3}$
D. $\dfrac{\pi }{2}$

Answer 1

Hint- We will be using an inscribed angle theorem to evaluate the base and height of the triangle which will help in finding the area of the triangle.

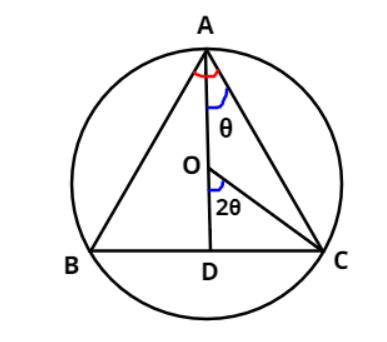
In the figure, $\vartriangle {\text{ABC}}$ is an isosceles triangle with ${\text{AB}} = {\text{AC}}$.
Also it is given that $\angle {\text{A}} = \angle {\text{BAC}} = 2\theta $ (shown in the figure as marked by red arc)
The centre of the circle is O and radius ${\text{OC}} = {\text{OA}} = a$
Now, let us draw an angle bisector AD from the vertex A of the isosceles triangle which divides $\angle {\text{A}} = \angle {\text{BAC}} = 2\theta $ into two equal angles i.e., $\angle {\text{BAD}} = \angle {\text{CAD}} = \dfrac{{2\theta }}{2} = \theta $.
According to the inscribed angle theorem, we can say that $\angle {\text{COD}}$ will be twice $\angle {\text{CAD}}$.
i.e., $\angle {\text{COD}} = 2\left( {\angle {\text{CAD}}} \right) = 2\theta $
In right angled triangle ODC,
$\cos \left( {2\theta } \right) = \dfrac{{{\text{Base}}}}{{{\text{Hypotenuse}}}} = \dfrac{{{\text{OD}}}}{{{\text{OC}}}} = \dfrac{{{\text{OD}}}}{a} \Rightarrow {\text{OD}} = a\left[ {\cos \left( {2\theta } \right)} \right]$
Also, \[\sin \left( {2\theta } \right) = \dfrac{{{\text{Perpendicular}}}}{{{\text{Hypotenuse}}}} = \dfrac{{{\text{DC}}}}{{{\text{OC}}}} = \dfrac{{{\text{DC}}}}{a} \Rightarrow {\text{DC}} = a\left[ {\sin \left( {2\theta } \right)} \right]\]
Now, ${\text{BC}} = 2\left( {{\text{DC}}} \right) = 2a\left[ {\sin \left( {2\theta } \right)} \right]$ and ${\text{AD}} = {\text{OD}} + {\text{OA}} = a\left[ {\cos \left( {2\theta } \right)} \right] + a = a\left[ {\cos \left( {2\theta } \right) + 1} \right]$
As we know that ${\text{Area of a triangle}} = \dfrac{1}{2} \times \left( {{\text{Base}}} \right) \times \left( {{\text{Height}}} \right)$
${\text{Area of }}\vartriangle {\text{ABC}}$, ${\text{A}} = \dfrac{1}{2} \times \left( {{\text{BC}}} \right) \times \left( {{\text{AD}}} \right) = \dfrac{1}{2} \times \left( {2a\left[ {\sin \left( {2\theta } \right)} \right]} \right) \times \left( {a\left[ {\cos \left( {2\theta } \right) + 1} \right]} \right) = {a^2}\left[ {\sin \left( {2\theta } \right)\cos \left( {2\theta } \right) + \sin \left( {2\theta } \right)} \right]$
Also we know that $\sin \left( {2\alpha } \right) = 2\left( {\sin \alpha } \right)\left( {\cos \alpha } \right) \Rightarrow \left( {\sin \alpha } \right)\left( {\cos \alpha } \right) = \dfrac{{\sin \left( {2\alpha } \right)}}{2}$
\[ \Rightarrow {\text{A}} = {a^2}\left[ {\sin \left( {2\theta } \right)\cos \left( {2\theta } \right) + \sin \left( {2\theta } \right)} \right] \Rightarrow {\text{A}} = {a^2}\left[ {\dfrac{{\sin \left( {4\theta } \right)}}{2} + \sin \left( {2\theta } \right)} \right]\]
Now differentiating above equation with respect to $\theta $ both sides, we get
\[
  \dfrac{{d{\text{A}}}}{{d\theta }} = \dfrac{{d\left\{ {{a^2}\left[ {\dfrac{{\sin \left( {4\theta } \right)}}{2} + \sin \left( {2\theta } \right)} \right]} \right\}}}{{d\theta }} = {a^2}\dfrac{{d\left[ {\dfrac{{\sin \left( {4\theta } \right)}}{2} + \sin \left( {2\theta } \right)} \right]}}{{d\theta }} = {a^2}\left[ {\dfrac{{4\cos \left( {4\theta } \right)}}{2} + 2\cos \left( {2\theta } \right)} \right] \\
   \Rightarrow \dfrac{{d{\text{A}}}}{{d\theta }} = {a^2}\left[ {2\cos \left( {4\theta } \right) + 2\cos \left( {2\theta } \right)} \right] \Rightarrow \dfrac{{d{\text{A}}}}{{d\theta }} = 2{a^2}\left[ {\cos \left( {4\theta } \right) + \cos \left( {2\theta } \right)} \right]{\text{ }} \to (1{\text{)}} \\
 \]
Now, for area of the triangle to be maximum put \[\dfrac{{d{\text{A}}}}{{d\theta }} = 0\]
\[ \Rightarrow 0 = 2{a^2}\left[ {\cos \left( {4\theta } \right) + \cos \left( {2\theta } \right)} \right] \Rightarrow \cos \left( {4\theta } \right) + \cos \left( {2\theta } \right) = 0 \Rightarrow \theta = \dfrac{\pi }{2},\dfrac{\pi }{6}\]
Now, differentiating equation (1) again with respect to $\theta $, we have
\[
   \Rightarrow \dfrac{{{d^2}{\text{A}}}}{{d{\theta ^2}}} = \dfrac{{d\left\{ {2{a^2}\left[ {\cos \left( {4\theta } \right) + \cos \left( {2\theta } \right)} \right]} \right\}}}{{d\theta }} = 2{a^2}\dfrac{{d\left[ {\cos \left( {4\theta } \right) + \cos \left( {2\theta } \right)} \right]}}{{d\theta }} = 2{a^2}\left[ { - 4\sin \left( {4\theta } \right) - 2\sin \left( {2\theta } \right)} \right] \\
   \Rightarrow \dfrac{{{d^2}{\text{A}}}}{{d{\theta ^2}}} = - 4{a^2}\left[ {2\sin \left( {4\theta } \right) + \sin \left( {2\theta } \right)} \right] \\
 \]
For \[\theta = \dfrac{\pi }{2}\], \[\dfrac{{{d^2}{\text{A}}}}{{d{\theta ^2}}} = - 4{a^2}\left[ {2\sin \left( {4 \times \dfrac{\pi }{2}} \right) + \sin \left( {2 \times \dfrac{\pi }{2}} \right)} \right] = - 4{a^2}\left[ {2\sin \left( {2\pi } \right) + \sin \left( \pi \right)} \right] = - 4{a^2}\left[ {2 \times 0 + 0} \right] = 0\]
For \[\theta = \dfrac{\pi }{6}\], \[\dfrac{{{d^2}{\text{A}}}}{{d{\theta ^2}}} = - 4{a^2}\left[ {2\sin \left( {4 \times \dfrac{\pi }{6}} \right) + \sin \left( {2 \times \dfrac{\pi }{6}} \right)} \right] = - 4{a^2}\left[ {2\sin \left( {\dfrac{{2\pi }}{3}} \right) + \sin \left( {\dfrac{\pi }{3}} \right)} \right] = - 4{a^2}\left[ {2 \times \dfrac{{\sqrt 3 }}{2} + \dfrac{{\sqrt 3 }}{2}} \right] = - 6\sqrt 3 {a^2}\]
As, we know that area of the triangle will be maximum where \[\dfrac{{{d^2}{\text{A}}}}{{d{\theta ^2}}} < 0\] i.e., will be negative .
So, at \[\theta = \dfrac{\pi }{6}\], the area of the given triangle is maximum.
Therefore, option A is correct.


Note- The inscribed angle theorem states that an angle $\theta $ inscribed in a circle is half of the central angle $2\theta $ that subtends the same arc on the circle. Also, here For \[\theta = \dfrac{\pi }{2}\], the double derivative of the area of the triangle comes out to be zero which means it is an inflection point.