Questions & Answers
Question
AnswersGive an example for which $ A \cdot B = C \cdot B $ but $ A \ne C $
Answer
Verified92.4k+ views
Hint: In order to prove the above statement, we will assume the vectors in the different directions. To prove the statement, we can assume the set of two vectors is perpendicular to each other. This will help us to find the scalar product easily as the value of angle becomes $ {90^ \circ } $ . This question is based on the assumptions.
Complete step-by-step answer:
The following is the schematic diagram expressing the vectors and their relations.
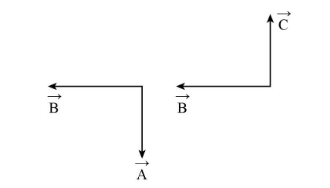
We will assume that $ A $ is perpendicular to $ B $ .
Now, we will assume $ B $ along the west direction. We also assume $ B $ is perpendicular to $ C $ , such that $ A $ is along south direction and $ C $ is along north direction.
If $ A $ is perpendicular to $ B $ then their scalar product must be zero. This can be expressed as,
$ A \cdot B = \left| A \right|\,\left| B \right|\,\cos \theta $
Since, $ A $ and $ B $ are perpendicular, $ \theta $ is equal to $ {90^ \circ } $ . Substituting the value of $ \theta $ in the above expression, we get,
$ A \cdot B = 0 $
If $ B $ is perpendicular to $ C $ then their scalar product must be zero. This can be expressed as,
$ B \cdot C = \left| B \right|\,\left| C \right|\,\cos \theta $
Since, $ B $ and $ C $ are perpendicular, $ \theta $ is equal to $ {90^ \circ } $ . Substituting the value of $ \theta $ in the above expression, we get,
$ B \cdot C = 0 $
Hence we can say that $ A \cdot B = B \cdot C = 0 $
But $ A $ and $ C $ are in the direction south and north respectively, Hence $ A \ne C $ .
Hence, it Is proved.
Note: If the two vectors are perpendicular to each other then their scalar product comes out to be zero. As at $ {90^ \circ } $ the value of cosine becomes zero. Using this, we can prove the given statements. Also, vectors have both magnitude and direction. Hence, for two vectors to be equal their magnitude and direction both must be the same.
Complete step-by-step answer:
The following is the schematic diagram expressing the vectors and their relations.
We will assume that $ A $ is perpendicular to $ B $ .
Now, we will assume $ B $ along the west direction. We also assume $ B $ is perpendicular to $ C $ , such that $ A $ is along south direction and $ C $ is along north direction.
If $ A $ is perpendicular to $ B $ then their scalar product must be zero. This can be expressed as,
$ A \cdot B = \left| A \right|\,\left| B \right|\,\cos \theta $
Since, $ A $ and $ B $ are perpendicular, $ \theta $ is equal to $ {90^ \circ } $ . Substituting the value of $ \theta $ in the above expression, we get,
$ A \cdot B = 0 $
If $ B $ is perpendicular to $ C $ then their scalar product must be zero. This can be expressed as,
$ B \cdot C = \left| B \right|\,\left| C \right|\,\cos \theta $
Since, $ B $ and $ C $ are perpendicular, $ \theta $ is equal to $ {90^ \circ } $ . Substituting the value of $ \theta $ in the above expression, we get,
$ B \cdot C = 0 $
Hence we can say that $ A \cdot B = B \cdot C = 0 $
But $ A $ and $ C $ are in the direction south and north respectively, Hence $ A \ne C $ .
Hence, it Is proved.
Note: If the two vectors are perpendicular to each other then their scalar product comes out to be zero. As at $ {90^ \circ } $ the value of cosine becomes zero. Using this, we can prove the given statements. Also, vectors have both magnitude and direction. Hence, for two vectors to be equal their magnitude and direction both must be the same.
Students Also Read