Question

From a well shuffled pack of $52$ cards , a cards is picked at random , find the probability that the card picked
a. Is either a queen or a red card
  (i) Depict the probability through venn diagram
b. Neither jack or spade
   (ii) Depict the probability through venn diagram

Answer 1

Hint:
Probability of event is equal to $\dfrac{{{\text{Favourable outcomes }}}}{{{\text{Total number of outcomes }}}}$ In the part (i) Total number of red cards in a deck of card is $13 + 13 = 26$ ,Total queens are $4$ in which $2$ are red and $2$ are black.
In the part (ii) Total number of Spade cards in a deck of cards is $13$ Total Jacks are $4$ in which $1$ are spade and $3$ are non- spade.

Complete step by step solution:
In this question we have to find the probability of a well shuffled pack of $52$ cards ,
In the part (i)
It is given that the Is either a queen or a red card So ,
Total number of cards in a pack $52$
Total number of red cards in a deck of card is $13 + 13 = 26$
Total queens are $4$ in which $2$ are red and $2$ are black.
Total number of red cards and queens is $26 + 2 = 28$
Now for the probability of event = $\dfrac{{{\text{Favourable outcomes }}}}{{{\text{Total number of outcomes }}}}$

Favourable outcomes = $28$ Total number of outcomes =$52$
Probability = $\dfrac{{28}}{{52}}$ = $0.5384$
Now for the venn diagram

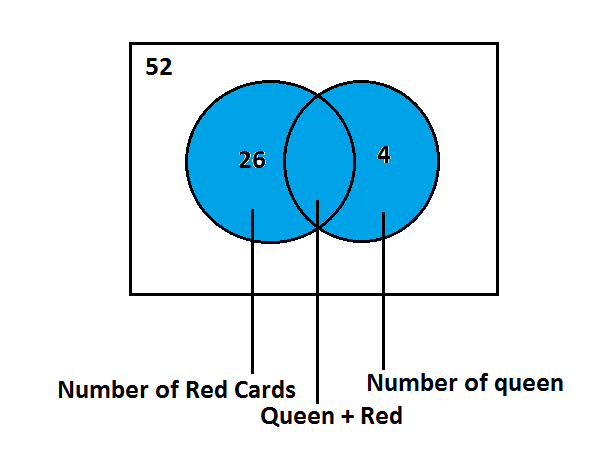
So from the venn diagram Probability is equal $\dfrac{{{\text{Shaded Region }}}}{{{\text{Total area}}}}$ that is equal to $\dfrac{{28}}{{52}}$= $0.5384$
In the part (ii) Probability we have to find neither jack nor spade
Total number of cards in a pack $52$
Total number of Spade cards in a deck of card is $13$
Total Jacks are $4$ in which $1$ are spade and $3$ are non- spade
Total number of spade card + Jack cards is $13 + 3 = 16$
Neither spade nor Jack cards = $52 - 16 = 36$
Now for the probability of event = $\dfrac{{{\text{Favourable outcomes }}}}{{{\text{Total number of outcomes }}}}$

Favourable outcomes = $36$ Total number of outcomes =$52$
Probability = $\dfrac{{36}}{{52}}$ = $0.72$
Now for the venn diagram

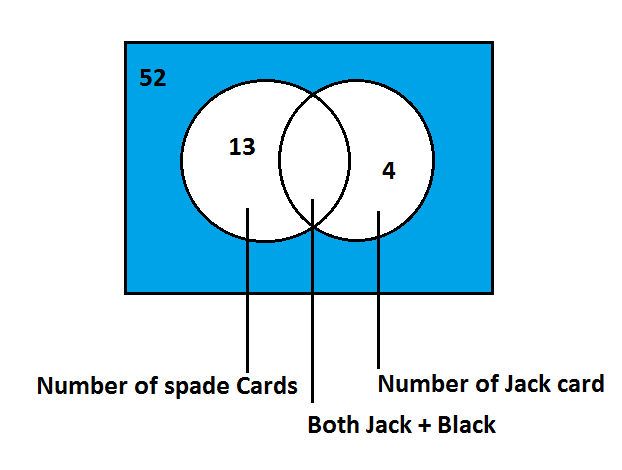So from the venn diagram Probability is equal $\dfrac{{{\text{Shaded Region }}}}{{{\text{Total area}}}}$ that is equal to $\dfrac{{36}}{{52}}$= $0.72$

Note:
In a deck of cards , All cards are divided into 4 suits. There are two black suits — spades and clubs and two red suits — hearts and diamonds.
Probability of any event always lies between $0$ to $1$. If your answer comes apart from this then cross check it.