Answer
Verified431.7k+ views
Hint: We start solving the problem by drawing the figure representing the given figure. We then make use of the fact that the slope form of the equation of the tangent to the parabola ${{y}^{2}}=4ax$ is $y=mx+\dfrac{a}{m}\Leftrightarrow mx-y+\dfrac{a}{m}=0$. We then apply the fact that the perpendicular distance from the centre of the circle to any of its tangent is equal to its radius to get the slope of tangent. We then find the equations of the chord of contact to the given circle and parabola. We then find the points of intersections of these chords with the tangents which are the vertices of the quadrilateral. We then make use of the fact that the area of the quadrilateral with vertices $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$, $\left( {{x}_{3}},{{y}_{3}} \right)$ and $\left( {{x}_{4}},{{y}_{4}} \right)$ is $\Delta =\dfrac{1}{2}\left| \begin{matrix}
{{x}_{1}}-{{x}_{3}} & {{x}_{2}}-{{x}_{4}} \\
{{y}_{1}}-{{y}_{3}} & {{y}_{2}}-{{y}_{4}} \\
\end{matrix} \right|$. We then make the necessary calculations to get the required value of the area of the quadrilateral.
Complete answer:
According to the problem, we are given that common tangents were drawn to the circle ${{x}^{2}}+{{y}^{2}}=\dfrac{{{a}^{2}}}{2}$ and the parabola ${{y}^{2}}=4ax$ from point A. We need to find the area of the quadrilateral formed by the common tangents, the chord of contact of the circle and the chord of contact of the parabola.
Let us draw the figure representing the given information.
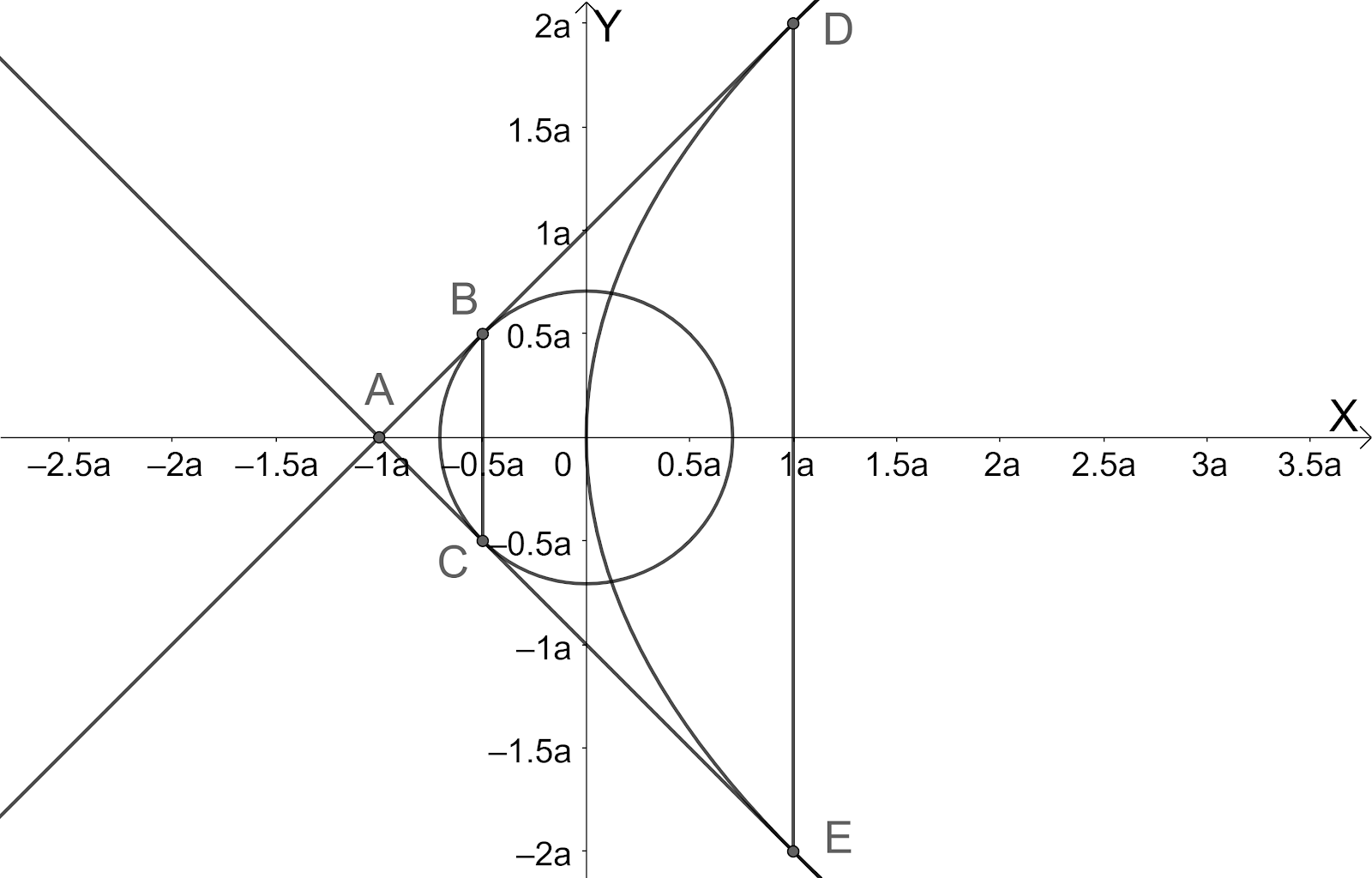
We know that the slope form of the equation of the tangent to the parabola ${{y}^{2}}=4ax$ is $y=mx+\dfrac{a}{m}\Leftrightarrow mx-y+\dfrac{a}{m}=0$. But this is also tangent to the circle ${{x}^{2}}+{{y}^{2}}=\dfrac{{{a}^{2}}}{2}$.
We know that the perpendicular distance from the centre of the circle to any of its tangent is equal to its radius.
So, we get $\dfrac{a}{\sqrt{2}}=\dfrac{\left| m\left( 0 \right)-0+\dfrac{a}{m} \right|}{\sqrt{{{m}^{2}}+{{\left( -1 \right)}^{2}}}}$.
$\Rightarrow \dfrac{a}{\sqrt{2}}=\dfrac{\left| \dfrac{a}{m} \right|}{\sqrt{{{m}^{2}}+1}}$.
Let us square on both sides.
\[\Rightarrow {{\left( \dfrac{a}{\sqrt{2}} \right)}^{2}}={{\left( \dfrac{\left| \dfrac{a}{m} \right|}{\sqrt{{{m}^{2}}+1}} \right)}^{2}}\].
\[\Rightarrow \dfrac{{{a}^{2}}}{2}=\dfrac{\dfrac{{{a}^{2}}}{{{m}^{2}}}}{{{m}^{2}}+1}\].
\[\Rightarrow \dfrac{{{a}^{2}}}{2}=\dfrac{{{a}^{2}}}{{{m}^{2}}\left( {{m}^{2}}+1 \right)}\].
\[\Rightarrow {{m}^{4}}+{{m}^{2}}=2\].
\[\Rightarrow {{m}^{4}}+{{m}^{2}}-2=0\].
\[\Rightarrow {{m}^{4}}+2{{m}^{2}}-{{m}^{2}}-2=0\].
\[\Rightarrow {{m}^{2}}\left( {{m}^{2}}+2 \right)-1\left( {{m}^{2}}+2 \right)=0\].
\[\Rightarrow \left( {{m}^{2}}-1 \right)\left( {{m}^{2}}+2 \right)=0\].
We know that ${{m}^{2}}+2>0$. So, we have ${{m}^{2}}-1=0$.
$\Rightarrow {{m}^{2}}=1$.
$\Rightarrow m=\pm 1$.
So, the equations of the tangents are $y=\pm \left( x+a \right)$ ---(1).
Let us find the point of intersection of these tangents.
So, we have $-\left( x+a \right)=+\left( x+a \right)$.
$\Rightarrow -x-a=x+a$.
$\Rightarrow -a-a=x+x$.
$\Rightarrow 2x=-2a$.
$\Rightarrow x=-a$ ---(2).
Let us substitute equation (2) in equation (1).
$\Rightarrow y=\pm \left( -a+a \right)$.
$\Rightarrow y=\pm \left( 0 \right)$.
$\Rightarrow y=0$.
So, the intersection point of the tangents is $A\left( -a,0 \right)$ ---(3).
We know that the equation of the chord of contact for a circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ is defined as $x{{x}_{1}}+y{{y}_{1}}+g\left( x+{{x}_{1}} \right)+f\left( y+{{y}_{1}} \right)+c=0$.
So, we get the chord of contact BC from the point $A\left( -a,0 \right)$ as $x\left( -a \right)+y\left( 0 \right)=\dfrac{{{a}^{2}}}{2}$.
$\Rightarrow -xa=\dfrac{{{a}^{2}}}{2}$.
$\Rightarrow x=\dfrac{-a}{2}$ ---(4).
Now, let us find the points of intersection chord of contact $x=\dfrac{-a}{2}$ with the tangents $y=\pm \left( x+a \right)$.
So, we have $y=\pm \left( \dfrac{-a}{2}+a \right)$.
$\Rightarrow y=\pm \left( \dfrac{a}{2} \right)$.
So, the points of intersection chord of contact $x=\dfrac{-a}{2}$ with the tangents $y=\pm \left( x+a \right)$ are $B\left( \dfrac{-a}{2},\dfrac{a}{2} \right)$ and $C\left( \dfrac{-a}{2},\dfrac{-a}{2} \right)$ ---(5).
We know that the equation of the chord of contact for a circle ${{y}^{2}}=4ax$ from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ is defined as $y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)$.
So, we get the chord of contact DE from point $A\left( -a,0 \right)$ as $y\left( 0 \right)=2a\left( x-a \right)$.
$\Rightarrow 0=2a\left( x-a \right)$.
$\Rightarrow x-a=0$.
$\Rightarrow x=a$ ---(6).
Now, let us find the points of intersection chord of contact $x=a$ with the tangents $y=\pm \left( x+a \right)$.
So, we have $y=\pm \left( a+a \right)$.
$\Rightarrow y=\pm \left( 2a \right)$.
So, the points of intersection chord of contact $x=a$ with the tangents $y=\pm \left( x+a \right)$ are $D\left( a,2a \right)$ and $E\left( a,-2a \right)$ ---(7).
Now, let us find the area of the quadrilateral $BCED$ whose vertices are $B\left( \dfrac{-a}{2},\dfrac{a}{2} \right)$, $C\left( \dfrac{-a}{2},\dfrac{-a}{2} \right)$, $E\left( a,-2a \right)$ and $D\left( a,2a \right)$.
We know that the area of the quadrilateral with vertices $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$, $\left( {{x}_{3}},{{y}_{3}} \right)$ and $\left( {{x}_{4}},{{y}_{4}} \right)$ is $\Delta =\dfrac{1}{2}\left| \begin{matrix}
{{x}_{1}}-{{x}_{3}} & {{x}_{2}}-{{x}_{4}} \\
{{y}_{1}}-{{y}_{3}} & {{y}_{2}}-{{y}_{4}} \\
\end{matrix} \right|$.
So, we have $\Delta =\dfrac{1}{2}\left| \begin{matrix}
\dfrac{-a}{2}-a & \dfrac{-a}{2}-a \\
\dfrac{a}{2}+2a & \dfrac{-a}{2}-2a \\
\end{matrix} \right|$.
$\Rightarrow \Delta =\dfrac{1}{2}\left| \begin{matrix}
\dfrac{-3a}{2} & \dfrac{-3a}{2} \\
\dfrac{5a}{2} & \dfrac{-5a}{2} \\
\end{matrix} \right|$ ---(8).
We know that $\left| \begin{matrix}
w & x \\
y & z \\
\end{matrix} \right|=\left( w\times z \right)-\left( y\times x \right)$. Let us use this in equation (8).
$\Rightarrow \Delta =\dfrac{1}{2}\times \left( \dfrac{-3a}{2}\times \dfrac{-5a}{2} \right)-\left( \dfrac{5a}{2}\times \dfrac{-3a}{2} \right)$.
$\Rightarrow \Delta =\dfrac{1}{2}\times \left( \dfrac{15{{a}^{2}}}{4} \right)-\left( \dfrac{-15{{a}^{2}}}{4} \right)$.
$\Rightarrow \Delta =\dfrac{1}{2}\times \left( \dfrac{15{{a}^{2}}}{4}+\dfrac{15{{a}^{2}}}{4} \right)$.
$\Rightarrow \Delta =\dfrac{1}{2}\times \left( \dfrac{30{{a}^{2}}}{4} \right)$.
$\Rightarrow \Delta =\dfrac{15{{a}^{2}}}{4}$ sq.units.
$\therefore $ We have found the area of the quadrilateral formed by the common tangents, the chord of contact of the circle and the chord of contact of the parabola as $\dfrac{15{{a}^{2}}}{4}$ sq.units.
Note:
We can see that the given problem contains a huge amount of calculation, so we need to perform each step carefully to avoid confusion and calculation mistakes. We can see that the quadrilateral formed is isosceles trapezium so, we can divide them into a combination of square and right-angle triangles to get the required area. We can also find the area of the obtained quadrilateral by dividing it into two triangles. Similarly, we can expect the problems to find the area of the quadrilateral formed with the normal of the tangents.
{{x}_{1}}-{{x}_{3}} & {{x}_{2}}-{{x}_{4}} \\
{{y}_{1}}-{{y}_{3}} & {{y}_{2}}-{{y}_{4}} \\
\end{matrix} \right|$. We then make the necessary calculations to get the required value of the area of the quadrilateral.
Complete answer:
According to the problem, we are given that common tangents were drawn to the circle ${{x}^{2}}+{{y}^{2}}=\dfrac{{{a}^{2}}}{2}$ and the parabola ${{y}^{2}}=4ax$ from point A. We need to find the area of the quadrilateral formed by the common tangents, the chord of contact of the circle and the chord of contact of the parabola.
Let us draw the figure representing the given information.
We know that the slope form of the equation of the tangent to the parabola ${{y}^{2}}=4ax$ is $y=mx+\dfrac{a}{m}\Leftrightarrow mx-y+\dfrac{a}{m}=0$. But this is also tangent to the circle ${{x}^{2}}+{{y}^{2}}=\dfrac{{{a}^{2}}}{2}$.
We know that the perpendicular distance from the centre of the circle to any of its tangent is equal to its radius.
So, we get $\dfrac{a}{\sqrt{2}}=\dfrac{\left| m\left( 0 \right)-0+\dfrac{a}{m} \right|}{\sqrt{{{m}^{2}}+{{\left( -1 \right)}^{2}}}}$.
$\Rightarrow \dfrac{a}{\sqrt{2}}=\dfrac{\left| \dfrac{a}{m} \right|}{\sqrt{{{m}^{2}}+1}}$.
Let us square on both sides.
\[\Rightarrow {{\left( \dfrac{a}{\sqrt{2}} \right)}^{2}}={{\left( \dfrac{\left| \dfrac{a}{m} \right|}{\sqrt{{{m}^{2}}+1}} \right)}^{2}}\].
\[\Rightarrow \dfrac{{{a}^{2}}}{2}=\dfrac{\dfrac{{{a}^{2}}}{{{m}^{2}}}}{{{m}^{2}}+1}\].
\[\Rightarrow \dfrac{{{a}^{2}}}{2}=\dfrac{{{a}^{2}}}{{{m}^{2}}\left( {{m}^{2}}+1 \right)}\].
\[\Rightarrow {{m}^{4}}+{{m}^{2}}=2\].
\[\Rightarrow {{m}^{4}}+{{m}^{2}}-2=0\].
\[\Rightarrow {{m}^{4}}+2{{m}^{2}}-{{m}^{2}}-2=0\].
\[\Rightarrow {{m}^{2}}\left( {{m}^{2}}+2 \right)-1\left( {{m}^{2}}+2 \right)=0\].
\[\Rightarrow \left( {{m}^{2}}-1 \right)\left( {{m}^{2}}+2 \right)=0\].
We know that ${{m}^{2}}+2>0$. So, we have ${{m}^{2}}-1=0$.
$\Rightarrow {{m}^{2}}=1$.
$\Rightarrow m=\pm 1$.
So, the equations of the tangents are $y=\pm \left( x+a \right)$ ---(1).
Let us find the point of intersection of these tangents.
So, we have $-\left( x+a \right)=+\left( x+a \right)$.
$\Rightarrow -x-a=x+a$.
$\Rightarrow -a-a=x+x$.
$\Rightarrow 2x=-2a$.
$\Rightarrow x=-a$ ---(2).
Let us substitute equation (2) in equation (1).
$\Rightarrow y=\pm \left( -a+a \right)$.
$\Rightarrow y=\pm \left( 0 \right)$.
$\Rightarrow y=0$.
So, the intersection point of the tangents is $A\left( -a,0 \right)$ ---(3).
We know that the equation of the chord of contact for a circle ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ is defined as $x{{x}_{1}}+y{{y}_{1}}+g\left( x+{{x}_{1}} \right)+f\left( y+{{y}_{1}} \right)+c=0$.
So, we get the chord of contact BC from the point $A\left( -a,0 \right)$ as $x\left( -a \right)+y\left( 0 \right)=\dfrac{{{a}^{2}}}{2}$.
$\Rightarrow -xa=\dfrac{{{a}^{2}}}{2}$.
$\Rightarrow x=\dfrac{-a}{2}$ ---(4).
Now, let us find the points of intersection chord of contact $x=\dfrac{-a}{2}$ with the tangents $y=\pm \left( x+a \right)$.
So, we have $y=\pm \left( \dfrac{-a}{2}+a \right)$.
$\Rightarrow y=\pm \left( \dfrac{a}{2} \right)$.
So, the points of intersection chord of contact $x=\dfrac{-a}{2}$ with the tangents $y=\pm \left( x+a \right)$ are $B\left( \dfrac{-a}{2},\dfrac{a}{2} \right)$ and $C\left( \dfrac{-a}{2},\dfrac{-a}{2} \right)$ ---(5).
We know that the equation of the chord of contact for a circle ${{y}^{2}}=4ax$ from the point $\left( {{x}_{1}},{{y}_{1}} \right)$ is defined as $y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)$.
So, we get the chord of contact DE from point $A\left( -a,0 \right)$ as $y\left( 0 \right)=2a\left( x-a \right)$.
$\Rightarrow 0=2a\left( x-a \right)$.
$\Rightarrow x-a=0$.
$\Rightarrow x=a$ ---(6).
Now, let us find the points of intersection chord of contact $x=a$ with the tangents $y=\pm \left( x+a \right)$.
So, we have $y=\pm \left( a+a \right)$.
$\Rightarrow y=\pm \left( 2a \right)$.
So, the points of intersection chord of contact $x=a$ with the tangents $y=\pm \left( x+a \right)$ are $D\left( a,2a \right)$ and $E\left( a,-2a \right)$ ---(7).
Now, let us find the area of the quadrilateral $BCED$ whose vertices are $B\left( \dfrac{-a}{2},\dfrac{a}{2} \right)$, $C\left( \dfrac{-a}{2},\dfrac{-a}{2} \right)$, $E\left( a,-2a \right)$ and $D\left( a,2a \right)$.
We know that the area of the quadrilateral with vertices $\left( {{x}_{1}},{{y}_{1}} \right)$, $\left( {{x}_{2}},{{y}_{2}} \right)$, $\left( {{x}_{3}},{{y}_{3}} \right)$ and $\left( {{x}_{4}},{{y}_{4}} \right)$ is $\Delta =\dfrac{1}{2}\left| \begin{matrix}
{{x}_{1}}-{{x}_{3}} & {{x}_{2}}-{{x}_{4}} \\
{{y}_{1}}-{{y}_{3}} & {{y}_{2}}-{{y}_{4}} \\
\end{matrix} \right|$.
So, we have $\Delta =\dfrac{1}{2}\left| \begin{matrix}
\dfrac{-a}{2}-a & \dfrac{-a}{2}-a \\
\dfrac{a}{2}+2a & \dfrac{-a}{2}-2a \\
\end{matrix} \right|$.
$\Rightarrow \Delta =\dfrac{1}{2}\left| \begin{matrix}
\dfrac{-3a}{2} & \dfrac{-3a}{2} \\
\dfrac{5a}{2} & \dfrac{-5a}{2} \\
\end{matrix} \right|$ ---(8).
We know that $\left| \begin{matrix}
w & x \\
y & z \\
\end{matrix} \right|=\left( w\times z \right)-\left( y\times x \right)$. Let us use this in equation (8).
$\Rightarrow \Delta =\dfrac{1}{2}\times \left( \dfrac{-3a}{2}\times \dfrac{-5a}{2} \right)-\left( \dfrac{5a}{2}\times \dfrac{-3a}{2} \right)$.
$\Rightarrow \Delta =\dfrac{1}{2}\times \left( \dfrac{15{{a}^{2}}}{4} \right)-\left( \dfrac{-15{{a}^{2}}}{4} \right)$.
$\Rightarrow \Delta =\dfrac{1}{2}\times \left( \dfrac{15{{a}^{2}}}{4}+\dfrac{15{{a}^{2}}}{4} \right)$.
$\Rightarrow \Delta =\dfrac{1}{2}\times \left( \dfrac{30{{a}^{2}}}{4} \right)$.
$\Rightarrow \Delta =\dfrac{15{{a}^{2}}}{4}$ sq.units.
$\therefore $ We have found the area of the quadrilateral formed by the common tangents, the chord of contact of the circle and the chord of contact of the parabola as $\dfrac{15{{a}^{2}}}{4}$ sq.units.
Note:
We can see that the given problem contains a huge amount of calculation, so we need to perform each step carefully to avoid confusion and calculation mistakes. We can see that the quadrilateral formed is isosceles trapezium so, we can divide them into a combination of square and right-angle triangles to get the required area. We can also find the area of the obtained quadrilateral by dividing it into two triangles. Similarly, we can expect the problems to find the area of the quadrilateral formed with the normal of the tangents.
Recently Updated Pages
Fill in the blanks with suitable prepositions Break class 10 english CBSE
Fill in the blanks with suitable articles Tribune is class 10 english CBSE
Rearrange the following words and phrases to form a class 10 english CBSE
Select the opposite of the given word Permit aGive class 10 english CBSE
Fill in the blank with the most appropriate option class 10 english CBSE
Some places have oneline notices Which option is a class 10 english CBSE
Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE
How do you graph the function fx 4x class 9 maths CBSE
When was Karauli Praja Mandal established 11934 21936 class 10 social science CBSE
Which are the Top 10 Largest Countries of the World?
What is the definite integral of zero a constant b class 12 maths CBSE
Why is steel more elastic than rubber class 11 physics CBSE
Distinguish between the following Ferrous and nonferrous class 9 social science CBSE
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths
Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE