Question

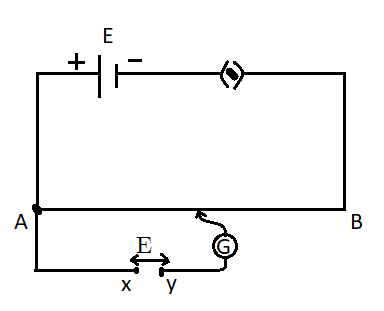
For the potentiometer circuit, shown in the given figure, points X and Y represent the two terminals of an unknown emf E. A student observed that when the jockey is moved from the end A to the end B of the potentiometer wire, the deflection in the galvanometer remains in the same direction. What are the two possible faults in the circuit that could result in this observation?
i) More
ii) Less
Than that at the end A. which of the two faults, listed above, would be there in the circuit? Give reasons in support of your answer in each case.

Answer 1

Hint: We know that galvanometer is used to measure the amount of current and voltage. In the given question, we are using a galvanometer with the potentiometer to indicate the null deflection point. We will assume the point of contact of the probe of the galvanometer with the potentiometer and then to find the null point, we will compare the potential at the point of contact to the emf given.

Complete step by step solution:

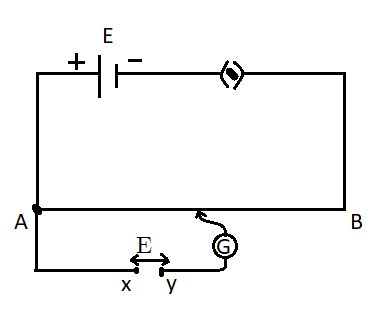
In the above potentiometer circuit, the unknown emf E is connected between X and Y and the jockey of the galvanometer is moved from point A to B.
Let us assume a point C where the probe of the galvanometer touches the wire.
When the potential ${E_{ac}}$ is equal and opposite of the emf \[{E'}\] , the galvanometer reading will be zero which means it will show the null point.
For null point, the two main conditions are:
The positive terminal of the unknown emf which is given to be \[{E'}\] must be connected to X terminal.
${E'} \leqslant E$ as ${E_{ac}} \leqslant {E_{ab}} = E$
The galvanometer will never show a null point if any of the above conditions is not satisfied.
Now, let us take the errors and compare the deflections at A and B.
If we violate the first condition which means if the positive terminal of unknown emf is connected to the Y terminal, then the net potential that the galvanometer will show is $\left( {{E_{ac}} + {E'}} \right)$ .
Due to this, the net potential or deflection in the galvanometer will be maximum which means the point B will give more reading.
Now, if we violate the second condition then ${E'} \geqslant E$ and the net potential across galvanometer will be $\left( {{E'} - {E_{ac}}} \right)$ . This will be maximum, when ${E_{ac}} = 0$ . It shows that point A will give more reading.

Note: In a potentiometer circuit when a galvanometer is used, it must satisfy the above two conditions, so that the galvanometer can show a null point. The net potential must be calculated to compare it with the unknown emf.