Question

For orthorhombic system axial ratios are $a \ne b \ne c$ and the axial angles are:
$
  (A) \alpha = \beta = \gamma \ne {90^ \circ } \\
  (B) \alpha = \beta = \gamma = {90^ \circ } \\
  (C) \alpha = \gamma = ,\beta \ne {90^ \circ } \\
  (D) \alpha \ne \beta \ne \gamma = {90^ \circ } \\
$

Answer 1

Hint:Axial ratios or lengths and axial angles are two important parameters of unit cell, axial length is the length or dimensions along the three edges a, b and c which may or may not be perpendicular and axial angles are the interaxial angles between pair of edges.

Complete answer:We know in a crystalline solid, constituent particles are arranged in a definite, three dimensional regular geometrical order along all the three axes, in which each particle is depicted as a lattice point. A three dimensional, regular arrangement of lattice points in space or in a crystal are called a crystal or space lattice.
After taking the axial lengths and interaxial angles into consideration various crystals are divided into 7 types of crystal systems also called crystal habits. One such crystal system is orthorhombic as given in the question above its edge lengths or ratios are $a \ne b \ne c$and inter-axial angles are $\alpha = \beta = \gamma = {90^ \circ }$. It has the structure like:

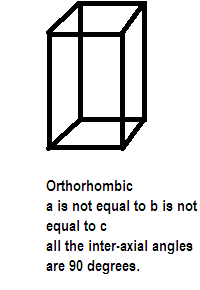
Further the seven crystal systems are classified on the basis of the unit cells present, a French mathematician has established fourteen different types of lattices called bravais lattice. Possible variations that the crystal system orthorhombic goes through are primitive, body centered, face centered and end centered unit cells which are different in terms of arrangement of their lattice points. Compounds showing orthorhombic crystal type are rhombic sulphur, barium sulphate, potassium sulphate and potassium nitrate etc.

Hence the correct option is (B).

Note: A crystal lattice has the following characteristics:
(i) Each point in a lattice is called a lattice site or point.
(ii) Each lattice point represents one constituent particle i.e atom, ion or molecule.
(iii) We join lattice points by straight lines to show the geometry of the lattice.