Question

For a concave mirror, paraxial rays are focused at a distance \[\dfrac{R}{2}\] from the pole and marginal rays are focused at a distance \[x\] from the pole, then \[R\] will be
(a) \[x = \dfrac{R}{2}\]
(b) \[x = - f\]
(c) \[x > \dfrac{R}{2}\]
(d) \[x < \dfrac{R}{2}\]

Answer 1

Hint: This question can be solved by understanding the meaning of paraxial rays and marginal rays. The ray which forms a small angle with respect to the optical axis is referred to as a paraxial ray whereas a marginal ray is a ray that passes through the maximum aperture of the spherical mirror. As the marginal mirror strikes the mirror at its edges they go through more deviation than paraxial rays.

Complete step-by-step solution:

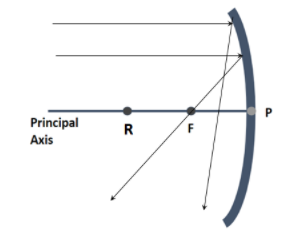
Since marginal rays have more deviation than when compared to paraxial rays as seen from the figure, it is understood that the paraxial and marginal rays meet at different points on the axis.
Since the paraxial rays are closer to the principal axis, once it strikes the mirror it is observed that the ray passes through the focus. Now we know that $f = \dfrac{R}{2}$. From the question also it is given that paraxial rays are focused at a distance \[\dfrac{R}{2}\] from the pole.
Since the marginal rays pass through the maximum aperture, the angle formed by the ray after it reflects from the mirror is large. Therefore we observe that the ray passes in between the pole and the focus. Hence we can see that the value of x, the distance from the pole for a marginal ray is less than \[\dfrac{R}{2}\].
Option d is the correct answer.

Note: Paraxial are the lines/rays situated alongside, or on each side of an axis. The marginal ray starts at the point where the object crosses the optical axis.