Question

Find the net force for any charge

Answer 1

Hint The force between two charged particles is calculated using the coulomb’s law which quantifies the attraction between two static charged particles. The force is proportional to the product of the charged particles and inversely proportional to the square of the distance between them. Using this formula we can find the net charge of the configuration.
In this solution we will be using the following formula,
Coulomb's law: $F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$ where $F$ is the force acting between two charged particles of charge ${q_1}$ and ${q_2}$ which have a distance $r$ between them.

Complete step by step answer
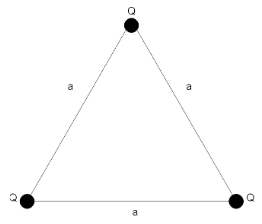
In the diagram given, we can see three charges that are at the corners of an equilateral triangle. We’ve been asked to find the net force on any charge and we can arbitrarily select any charge to find the force since the system is symmetrical and the force experienced by all the 3 charges will be the same.
So, let us select the bottom left charge. From the coulomb’s law, we know that the force between two charges can be written as
$\Rightarrow F = \dfrac{{k{q_1}{q_2}}}{{{r^2}}}$
So, for the bottom left charge, the force it will experience will be due to the other two identical charges which are situated at a distance $a$. So, the net force will be a sum of the forces due to these charges. So, we can write
$\Rightarrow F = \dfrac{{kQQ}}{{{a^2}}} + \dfrac{{kQQ}}{{{a^2}}} $
$\Rightarrow F = \dfrac{{2k{Q^2}}}{{{a^2}}} $

Note
The distance between any two point charges in the length of the line joining the two points which in our case is the length of the side of the triangle which has a length $a$. Since all the charges are identical, the net force experienced by any particle will be repulsive in nature.