
Find the equations to the common tangents of the circle \[{x^2} + {y^2} + 4ax = 0\] and parabola \[{y^2} = 4ax\]
Answer
582.3k+ views
Hint: From the given two equations we first try to find out the center of the circle and its radius. And then we have to find out if the parabola and the circle are touching each other or not. Thus we can find the result by observing the solution.
Complete step by step answer:
Here in this problem, we are given two equations, \[{x^2} + {y^2} + 4ax = 0\] and \[{y^2} = 4ax\]. Where one of them is a circle and the other is a parabola. We need to find the equation of common tangents of these two.
So, the equation of the circle is,
\[{x^2} + {y^2} + 4ax = 0\]
Adding \[4{a^2}\] to both sides we get,
\[ \Rightarrow {x^2} + 4ax + 4{a^2} + {y^2} = 4{a^2}\]
On applying \[{{\text{a}}^{\text{2}}}{\text{ + 2ab + }}{{\text{b}}^{\text{2}}}{\text{ = (a + b}}{{\text{)}}^{\text{2}}}\], we get,
\[ \Rightarrow {(x + 2a)^2} + {y^2} = 4{a^2}\]……(i)
So, we get the circle with center at \[( - 2a,0)\]and with radius \[2a\] units.
And we have the 2nd equation as, \[{y^2} = 4ax\] which is passing through the origin.
Now, if we try to plot them altogether, we get,
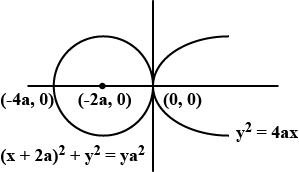
Now, from the figure, it is clearly visible that, the circle and the parabola are touching each other along the y-axis and it is the common tangent of these two given equations.
So, now, the equation of the common tangent is, \[x = 0\]
Note: In this given problem we focused on finding where the different figures are meeting each other and if they are at all touching each other or not. In these types of problems, if the figures are touching each other, our job becomes easier as the common tangent is always passing through their point of intersection.
Complete step by step answer:
Here in this problem, we are given two equations, \[{x^2} + {y^2} + 4ax = 0\] and \[{y^2} = 4ax\]. Where one of them is a circle and the other is a parabola. We need to find the equation of common tangents of these two.
So, the equation of the circle is,
\[{x^2} + {y^2} + 4ax = 0\]
Adding \[4{a^2}\] to both sides we get,
\[ \Rightarrow {x^2} + 4ax + 4{a^2} + {y^2} = 4{a^2}\]
On applying \[{{\text{a}}^{\text{2}}}{\text{ + 2ab + }}{{\text{b}}^{\text{2}}}{\text{ = (a + b}}{{\text{)}}^{\text{2}}}\], we get,
\[ \Rightarrow {(x + 2a)^2} + {y^2} = 4{a^2}\]……(i)
So, we get the circle with center at \[( - 2a,0)\]and with radius \[2a\] units.
And we have the 2nd equation as, \[{y^2} = 4ax\] which is passing through the origin.
Now, if we try to plot them altogether, we get,
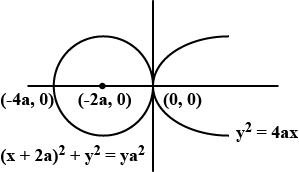
Now, from the figure, it is clearly visible that, the circle and the parabola are touching each other along the y-axis and it is the common tangent of these two given equations.
So, now, the equation of the common tangent is, \[x = 0\]
Note: In this given problem we focused on finding where the different figures are meeting each other and if they are at all touching each other or not. In these types of problems, if the figures are touching each other, our job becomes easier as the common tangent is always passing through their point of intersection.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Two Planoconcave lenses 1 and 2 of glass of refractive class 12 physics CBSE

The compound 2 methyl 2 butene on reaction with NaIO4 class 12 chemistry CBSE

Bacterial cell wall is made up of A Cellulose B Hemicellulose class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers

State the principle of an ac generator and explain class 12 physics CBSE




