Question

Find the domain and range of following real functions:
A) $f(x) = - \left| x \right|$
B) $f(x) = \sqrt {9 - {x^2}} $

Answer 1

Hint: According to given in the question we have to determine the domain and range of the real functions as given $f(x) = - \left| x \right|$and$f(x) = \sqrt {9 - {x^2}} $. So, first of all we have to understand about the domain which is explained below:
Domain: The domain of a function is the complete set of possible values of the independent variables and the domain is the set of all possible x –values which can make the given function work and will output all the real y-values.
Now, we have to understand about the range of a function which is explained below:
Range: As we know that function has input and outputs and the inputs are what we put in the function and the output are what come out and we call the set of outputs as the range for that function.
Now, we have to substitute the all values of x that should be real to obtain the output if the function to determine the domain and range for the given functions.

Formula used: $ \Rightarrow ({a^2} - {b^2}) = (a + b)(a - b)..............(A)$

Complete step-by-step solution:
Step 1: First of all we have to place all the value of x that should be $(x \in R)$where R is the real numbers means we will substitute all the real numbers as (2, 1, 0, -1, -2) to check for the domain for the domain of the function. Hence,
On substituting the value of x = 2,
$
   \Rightarrow f(2) = - \left| 2 \right| \\
   \Rightarrow f(2) = - 2
 $
Which is a real number.
Now, On substituting the value of x = 2,
$
   \Rightarrow f(1) = - \left| 1 \right| \\
   \Rightarrow f(1) = - 1
 $
Which is a real number.
Now, On substituting the value of x = 0,
$
   \Rightarrow f(0) = - \left| 0 \right| \\
   \Rightarrow f(0) = 0
 $
Which is a real number.
Now, On substituting the value of x = -1,
$
   \Rightarrow f( - 1) = - \left| { - 1} \right| \\
   \Rightarrow f( - 1) = - 1
 $
Which is a real number.
Now, On substituting the value of x = -2,
$
   \Rightarrow f( - 2) = - \left| { - 2} \right| \\
   \Rightarrow f( - 2) = - 2
 $
Which is a real number.
Here, value of domain (x) can be any real number hence, Domain = R which are all real number
Step 2: As obtained from step 1. We have obtained the range f(x) which is 0 or negative numbers, hence,
Range = $( - \infty ,0]$
Step 3: Now, we have to obtain the domain and range for the function (ii) $f(x) = \sqrt {9 - {x^2}} $so, to find that we have to solve the expression,
$
   = \sqrt {9 - {x^2}} \geqslant 0 \\
   = 9 - {x^2} \geqslant 0 \\
   = {x^2} - 9 \leqslant 0.................(1)
 $
Step 4: Now, to solve the expression (1) we have to use the formula (A) as mentioned in the solution hint.
$ = (x + 3)(x - 3) \leqslant 0$
Hence, the domain for the function $f(x) = \sqrt {9 - {x^2}} $is $x \in [ - 3,3]$
Step 5: Now, to obtain the range for the function we have to solve the equation $f(x) = \sqrt {9 - {x^2}} $but first of all we have to consider the equation as $y = \sqrt {9 - {x^2}} $now, on applying square on the both sides of the expression,
$
   \Rightarrow {y^2} = 9 - {x^2} \\
   \Rightarrow {x^2} + {y^2} = 9
 $
Which is an equation of circle hence, with the help of a graph of circle we can obtain the range for the given function. Hence,

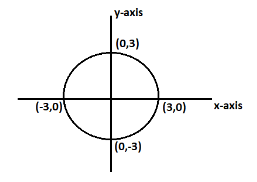
Range of the function is $x \in [ - 3,3]$

Hence, we have obtain the domain and range for the function (A)$f(x) = - \left| x \right|$which are Domain $x \in R$where, R is the all real numbers and Range = $( - \infty ,0]$
(B) $f(x) = \sqrt {9 - {x^2}} $the domain is $x \in [ - 3,3]$ and the range $x \in [ - 3,3]$

Note: When finding the domain we should remember that the number under a square root sign must be positive in the section and the denominator of a fraction never should be zero.
The range of a function may refer to either of two closely related concepts that are codomain of the function and the image of the function.