Question

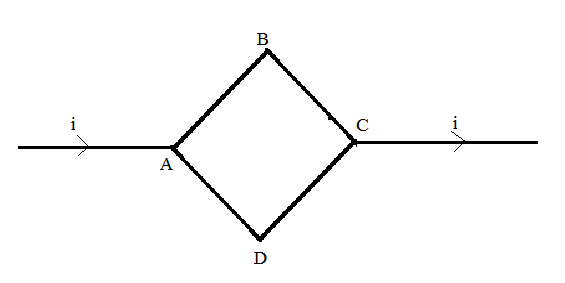
Figure shows a square loop ABCD with edge-length ‘a’. The resistance of the wire ABC is ‘r’, and that of ADC is ‘2r’. Find the magnetic field B at the center of the loop, assuming uniform wires.

Answer 1

Hint: In this question, we need to determine the magnetic field B at the center of the loop due to uniform wires. For this, we will follow the relation between the magnetic field and the current.

Complete step by step answer:
The resistance of the wire ABC is ‘r’ and of the wire, ADC is ‘2r’. Both the wires =have the same endpoints, and so, we can say that the wires are connected in parallel.
The total amount of current flowing through the circuit has been given as ‘i’.
Now, applying the current division rule in the given circuit to determine the amount of the current flowing through the wire ABC and ADC.
Current through the wire ABS is given as:
$
  {i_{ABC}} = \left( {\dfrac{i}{{r + 2r}}} \right)2r \\
   = \dfrac{{2i}}{3} \\
 $
Similarly, the amount of current passing through the wire ADC is given as:
$
  {i_{ADC}} = \left( {\dfrac{i}{{r + 2r}}} \right)r \\
   = \dfrac{i}{3} \\
 $

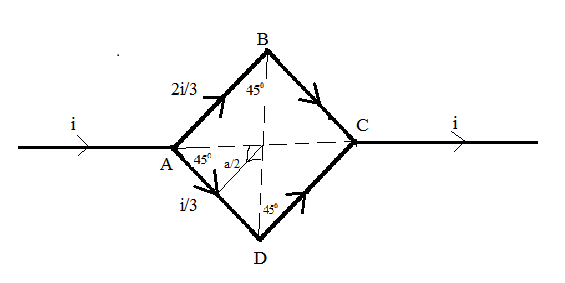
The magnetic field for the straight wire carrying current is given as $B = \dfrac{{{\mu _0}i}}{{4\pi d}}\left( {\sin {\theta _1} + \sin {\theta _2}} \right)$ where, ‘i’ is the amount of current flowing through the wire, ‘d’ is the perpendicular distance of the point where we need to evaluate the magnetic field and ${\theta _1}{\text{ and }}{\theta _2}$ are the angles made by the endpoints of the wire at the point where we need to evaluate the magnetic field.
For the wire ADC, an equal amount of current is flowing through the sub-parts AD and DC, and equal angles have been subtended at the center of the loop, i.e., 45 degrees. So, the total magnetic field at the center of the loop due to the wire ADC is given as:
\[
  {B_1} = 2 \times \dfrac{{{\mu _0}\left( {\dfrac{i}{3}} \right)}}{{4\pi \left( {\dfrac{a}{2}} \right)}}\left( {\sin {{45}^0} + \sin {{45}^0}} \right) \\
   = 2 \times \dfrac{{{\mu _0}i}}{{6\pi a}}\left( {\dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }}} \right) \\
   = \dfrac{{\sqrt 2 {\mu _0}i}}{{3\pi a}} - - - - (i) \\
 \]
Again, for the wire ABC, an equal amount of current is flowing through the sub-parts AD and DC, and equal angles have been subtended at the center of the loop, i.e., 45 degrees. So, the total magnetic field at the center of the loop due to the wire ADC is given as:
\[
  {B_2} = 2 \times \dfrac{{{\mu _0}\left( {\dfrac{{2i}}{3}} \right)}}{{4\pi \left( {\dfrac{a}{2}} \right)}}\left( {\sin {{45}^0} + \sin {{45}^0}} \right) \\
   = 2 \times \dfrac{{{\mu _0}i}}{{3\pi a}}\left( {\dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }}} \right) \\
   = \dfrac{{2\sqrt 2 {\mu _0}i}}{{3\pi a}} - - - - (ii) \\
 \]
Following Fleming’s right-hand rule, the magnetic field at the center of the loop due to the wire ADC is outwards, and due to the wire, ABC is inwards. Hence, the net magnetic field is the resultant of the difference in the magnetic field due to the wire ABC and the wire ADC.
\[
  {B_{net}} = {B_2} - {B_1} \\
   = \dfrac{{2\sqrt 2 {\mu _0}i}}{{3\pi a}} - \dfrac{{\sqrt 2 {\mu _0}i}}{{3\pi a}} \\
   = \dfrac{{\sqrt 2 {\mu _0}i}}{{3\pi a}} \\
 \]
Hence, the magnetic field B at the center of the loop is \[\dfrac{{\sqrt 2 {\mu _0}i}}{{3\pi a}}\].

Note:Students should be very careful while substituting the values of the angle subtended at the desired point of the magnetic field. Moreover, here the direction of the current in both the wires is opposite, and so, the net magnetic field is the difference between the two.