Question

Figure shows a fixed square frame of wire having a total resistance $r$ placed coplanar with a long, straight wire. The wire carries a current $i$ given by $i={{i}_{2}}\cos \left( \dfrac{2\pi t}{T} \right)$. Find-
(a). the flux of the magnetic field through the square frame
(b). the emf induced in the frame
(c). the heat developed in the frame in the time interval 0 to $10T$

Answer 1

Hint: As each element of the square loop is at a different distance from the current carrying wire, flux associated with each will be different. Therefore, we calculate for an element and then integrate it for the whole square. The emf generated is opposite to the direction of current but directly proportional to the rate of change of current.

Formulas Used:
$B=\dfrac{{{\mu }_{0}}I}{2\pi R}$
$\phi =BA\cos \theta $
$e=-\dfrac{d\phi }{dt}$

Complete step-by-step solution:

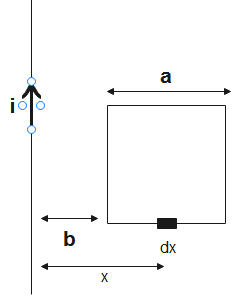
Let us consider a strip of wire on the square of thickness $dx$. Its distance from the wire is $x$.
When current flows through the wire, a magnetic field is developed around it. The magnetic field intensity, $B$ due to a long wire is given by-
$B=\dfrac{{{\mu }_{0}}I}{2\pi R}$
Here, ${{\mu }_{0}}$ is permeability of free space
$I$ is the current flowing through the wire
$R$ is distance from wire
Therefore magnetic field on strip $dx$ will be-
$B=\dfrac{{{\mu }_{0}}i}{2\pi x}$ - (1)
Flux associated with an area is the number of magnetic field lines associated with it.
Flux,$\phi $ passing through an area is given by
$\phi =BA\cos \theta $
Here, $A$ is the area of cross section
$\theta $ is the angle between area vector and Flux passing through $dx$ is given by-
$\begin{align}
  & \int\limits_{0}^{\phi }{\phi }=\int\limits_{b}^{b+a}{B\,(adx)} \\
 & \Rightarrow \phi =\int\limits_{b}^{b+a}{\dfrac{{{\mu }_{0}}i}{2\pi x}(adx)} \\
 & \Rightarrow \phi =\dfrac{{{\mu }_{0}}ia}{2\pi }\int\limits_{b}^{b+a}{\dfrac{(dx)}{x}} \\
 & \Rightarrow \phi =\dfrac{{{\mu }_{0}}ia}{2\pi }{}_{b}^{b+a}\left[ \ln x \right] \\
 & \Rightarrow \phi =\dfrac{{{\mu }_{0}}ia}{2\pi }\left[ \ln b+a-\ln b \right] \\
\end{align}$
$\therefore \phi =\dfrac{{{\mu }_{0}}ia}{2\pi }\ln \dfrac{b+a}{b}$ - (1)
Therefore, the total flux associated with the square loop is $\dfrac{{{\mu }_{0}}ia}{2\pi }\left[ \ln \dfrac{b+a}{b} \right]$.
(b). We know that emf induced in the frame is given by-
$e=-\dfrac{d\phi }{dt}$
Substituting values from eq(1), we get,
$e=-\dfrac{d}{dt}\left( \dfrac{{{\mu }_{0}}ia}{2\pi }\left[ \ln \dfrac{b+a}{b} \right] \right)$
Given, $i={{i}_{2}}\cos \left( \dfrac{2\pi t}{T} \right)$ therefore,
$\begin{align}
  & e=-\dfrac{d}{dt}\left( \dfrac{{{\mu }_{0}}a{{i}_{2}}\cos \left( \dfrac{2\pi t}{T} \right)}{2\pi }\left[ \ln \dfrac{b+a}{b} \right] \right) \\
 & \Rightarrow e=-\dfrac{{{\mu }_{0}}a{{i}_{2}}}{2\pi }\left[ \ln \dfrac{b+a}{b} \right]\dfrac{d}{dt}\cos \left( \dfrac{2\pi t}{T} \right) \\
 & \Rightarrow e=-\dfrac{{{\mu }_{0}}a{{i}_{2}}}{2\pi }\left[ \ln \dfrac{b+a}{b} \right]\left( -\dfrac{2\pi }{T}\sin \left( \dfrac{2\pi t}{T} \right) \right) \\
\end{align}$
$\therefore e=\dfrac{{{\mu }_{0}}a{{i}_{2}}\left( \sin \left( \dfrac{2\pi t}{T} \right) \right)}{T}\left[ \ln \dfrac{b+a}{b} \right]$ - (2)
Therefore, the emf induced in the square loop is $\dfrac{{{\mu }_{0}}a{{i}_{2}}\left( \sin \left( \dfrac{2\pi t}{T} \right) \right)}{T}\left[ \ln \dfrac{b+a}{b} \right]$V
(c). the formula for heat is
$H=\dfrac{{{V}^{2}}}{R}dt$
Here, $V$ is the potential drop in the square loop
$R$ is the resistance
Substituting from eq (2), we get,
$\begin{align}
  & H=\dfrac{{{e}^{2}}}{r}dt \\
 & \Rightarrow H=\dfrac{1}{r}\left( \dfrac{{{\mu }_{0}}a{{i}_{2}}\left( \sin \left( \dfrac{2\pi t}{T} \right) \right)}{T}\left[ \ln \dfrac{b+a}{b} \right] \right)dt \\
 & \Rightarrow H=\dfrac{\mu _{0}^{2}{{a}^{2}}i_{2}^{2}}{r{{T}^{2}}}{{\ln }^{2}}\left[ \dfrac{b+a}{b} \right]{{\left( \sin \left( \dfrac{2\pi t}{T} \right) \right)}^{2}}dt \\
 & \Rightarrow H=\dfrac{\mu _{0}^{2}{{a}^{2}}i_{2}^{2}}{r{{T}^{2}}}{{\ln }^{2}}\left[ \dfrac{b+a}{b} \right]\left( {{\sin }^{2}}\left( \dfrac{2\pi t}{T} \right) \right)dt \\
 & \Rightarrow H=\dfrac{\mu _{0}^{2}{{a}^{2}}i_{2}^{2}4\pi }{r{{T}^{3}}}{{\ln }^{2}}\left[ \dfrac{b+a}{b} \right]\left( \sin \left( \dfrac{2\pi t}{T} \right)\cos \left( \dfrac{2\pi t}{T} \right) \right) \\
\end{align}$
$\therefore H=\dfrac{\mu _{0}^{2}{{a}^{2}}i_{2}^{2}4\pi }{r{{T}^{3}}}{{\ln }^{2}}\left[ \dfrac{b+a}{b} \right]\left( \sin \left( \dfrac{2\pi t}{T} \right)\cos \left( \dfrac{2\pi t}{T} \right) \right)$ - (3)

Therefore, the heat developed in the square loop is $\dfrac{\mu _{0}^{2}{{a}^{2}}i_{2}^{2}4\pi }{r{{T}^{3}}}{{\ln }^{2}}\left[ \dfrac{b+a}{b} \right]\left( \sin \left( \dfrac{2\pi t}{T} \right)\cos \left( \dfrac{2\pi t}{T} \right) \right)$

Therefore by eq(1), eq (2) and eq (3) the flux associated with the square loop is:-
$\phi =\dfrac{{{\mu }_{0}}ia}{2\pi }\ln \dfrac{b+a}{b}$.

Emf developed across its ends is:-
$e=\dfrac{{{\mu }_{0}}a{{i}_{2}}\left( \sin \left( \dfrac{2\pi t}{T} \right) \right)}{T}\left[ \ln \dfrac{b+a}{b} \right]$.

And heat generated is:-
$\dfrac{\mu _{0}^{2}{{a}^{2}}i_{2}^{2}4\pi }{r{{T}^{3}}}{{\ln }^{2}}\left[ \dfrac{b+a}{b} \right]\left( \sin \left( \dfrac{2\pi t}{T} \right)\cos \left( \dfrac{2\pi t}{T} \right) \right)$.

Note:
The direction of magnetic field due to current carrying wire is given by right hand thumb rule. If an area vector of a surface is perpendicular to the direction of magnetic field, there is no flux passing through it. Most of the energy of the square loop developed due to a potential difference at its ends is dissipated as heat.