Question

Explain with a neat diagram the principle, construction, and working of a cyclotron.

Answer 1

Hint: First we will discuss what a cyclotron is and the principle on which it works. After that, we discuss how a cyclotron is constructed and then explain how a cyclotron works and derive the time period of the revolution and time period of the oscillator. And then find the frequency of the oscillator.

Formula used:
$Bqv=\dfrac{m{{v}^{2}}}{r}$

Complete step-by-step solution:

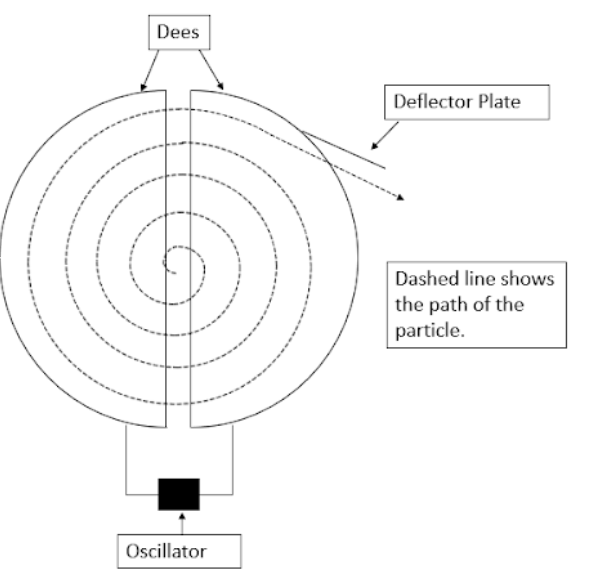
A cyclotron is a device used to accelerate charged particles to very high speeds. The principle on which a cyclotron relies is that a charged particle moving perpendicular to a magnetic field experiences a magnetic Lorentz force on it due to which the charged particles move in a circular path.
A cyclotron consists of a metallic hollow cylinder divided into two parts called Dees. The two Dees have a gap between them where a source of ions is placed. They are kept between a strong electromagnet such that the magnetic field acts along the length of the cylinder. The two Dees are connected to a high-frequency oscillator.
Let’s assume that the ion source produces a positive ion. So when the ion is produced it moves towards the Dee with negative polarity and moves through it and then when it comes out of the Dee, the polarity changes again due to which the particle accelerates and the particles with the higher velocity now move in a circle of larger radius. The radius of the motion of particles keeps on increasing like this and the particle moves in a spiral path of increasing radius as in the figure. When the particle reaches near the edge, it is taken out with the help of a deflector plate and then hits a target.
If we balance the magnetic force with the centripetal force, we get
$\begin{align}
  & Bqv=\dfrac{m{{v}^{2}}}{r} \\
 & \dfrac{v}{r}=\dfrac{Bq}{m} \\
\end{align}$
As we can see the ratio of velocity and radius remains constant. So, the time is taken to travel in one Dee(semicircle) will also remain the same. Time t for that will be
$t=\dfrac{\pi r}{v}=\dfrac{\pi m}{Bq}$
The time period of one revolution, as well as the oscillations of the oscillator, will be the same and be twice of t
$T=2t=\dfrac{2\pi m}{Bq}$
The frequency of the oscillator will then be
$\nu =\dfrac{1}{T}=\dfrac{Bq}{2\pi m}$
This condition is called the resonance condition of the cyclotron. At the end of the path, there is a window for the particle to go out and there is a deflector plate there which provides the necessary force to make the particle move in a straight line after it gets out.

Note: There are certain limitations of a cyclotron as well such that the size of the cyclotron limits the velocity to which the particle can be accelerated and it is hard to produce a uniform magnetic field over the complete Dee. Also, relativistic effects at high speeds disturb the resonance conditions.