Questions & Answers
Question
Answers
Related Questions
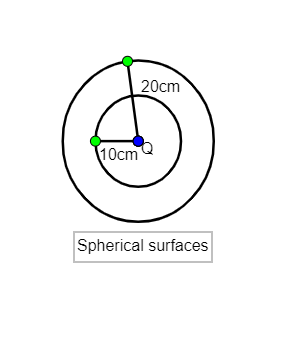
Electric charges are distributed in a small volume. The flux of the electric field through a spherical surface of radius 10cm surrounding the total charge is 25 V-m. The flux over a concentric sphere of radius 20 cm will be:
$A.$ 25V-m
$B.$ 50V-m
$C.$ 100V-m
$D.$ 200V-m
Answer
![Verified]()
Verified
Verified
Hint: The flux through a surface does not depend on its shape and size; it only depends upon the charge enclosed by the sphere of radius 10 cm and the sphere of radius 20 cm is same so the flux through them will also be the same.
Complete answer:
Values given to us are flux through a surface of 10cm is ${{\phi }_{10}}$=25 V-m
$Q_{en}^{10}$ is charge enclosed within a radius of 10cm
$Q_{en}^{20}$is the charge enclosed within a radius of 20cm
${{\phi }_{20}}$ is the flux through a surface of 20cm
Using Gauss’s law, ${{\phi }_{10}}=\dfrac{Q_{en}^{10}}{{{\in }_{0}}}$
Or $Q_{en}^{10}=25{{\in }_{0}}$
Here for flux of radius 20cm, $Q_{en}^{20}=Q_{en}^{10}=25{{\in }_{0}}$
Thus, ${{\phi }_{20}}=\dfrac{25{{\in }_{0}}}{{{\in }_{0}}}=25$V-m.
So, the correct answer is “Option A”.
Additional Information:
Laws of physics like the Gauss's law for magnetism and Gauss's law for gravity have a great mathematical similarity with the Gauss law. Any inverse-square law can be deducted to Gauss's law. For example, Gauss's law itself is quite equivalent to the inverse-square Coulomb's law and Gauss's law for gravity is quite equivalent to the inverse-square Newton's law of gravity.
Note:
Electric field passing through a given area at a particular time is known as electric flux. Electric flux is directly proportional to the number of electric field lines passing through that given area. If the electric field is uniform, the electric flux passing through a surface of vector area S is: \[\phi =E\cdot S=EScos\theta \], where E is the magnitude of the electric field having units of V/m, S is the area of the surface, and θ is the angle between the electric field lines and the normal to S. Electric flux is also related to Gauss law. Gauss Law states the net electric flux from a closed surface is equal to $\dfrac{1}{{{\in }_{0}}}$ times the net charge enclosed in that area. There are two forms of the Gauss law; the integral form and the differential form.
Complete answer:
Values given to us are flux through a surface of 10cm is ${{\phi }_{10}}$=25 V-m
$Q_{en}^{10}$ is charge enclosed within a radius of 10cm
$Q_{en}^{20}$is the charge enclosed within a radius of 20cm
${{\phi }_{20}}$ is the flux through a surface of 20cm
Using Gauss’s law, ${{\phi }_{10}}=\dfrac{Q_{en}^{10}}{{{\in }_{0}}}$
Or $Q_{en}^{10}=25{{\in }_{0}}$
Here for flux of radius 20cm, $Q_{en}^{20}=Q_{en}^{10}=25{{\in }_{0}}$
Thus, ${{\phi }_{20}}=\dfrac{25{{\in }_{0}}}{{{\in }_{0}}}=25$V-m.
So, the correct answer is “Option A”.
Additional Information:
Laws of physics like the Gauss's law for magnetism and Gauss's law for gravity have a great mathematical similarity with the Gauss law. Any inverse-square law can be deducted to Gauss's law. For example, Gauss's law itself is quite equivalent to the inverse-square Coulomb's law and Gauss's law for gravity is quite equivalent to the inverse-square Newton's law of gravity.
Note:
Electric field passing through a given area at a particular time is known as electric flux. Electric flux is directly proportional to the number of electric field lines passing through that given area. If the electric field is uniform, the electric flux passing through a surface of vector area S is: \[\phi =E\cdot S=EScos\theta \], where E is the magnitude of the electric field having units of V/m, S is the area of the surface, and θ is the angle between the electric field lines and the normal to S. Electric flux is also related to Gauss law. Gauss Law states the net electric flux from a closed surface is equal to $\dfrac{1}{{{\in }_{0}}}$ times the net charge enclosed in that area. There are two forms of the Gauss law; the integral form and the differential form.
Like this
Liked
-
LIVECourses
-
V PRO
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
-
NEET
-
NEET 2021
-
NEET 2022
-
-
CBSE
-
Class 6
-
Class 7
-
Class 8
-
Class 9
-
Class 10
-
Class 11
-
Class 12
-
-
ICSE
-
Class 9
-
Class 10
-
-
Maharashtra Board
-
Class 9
-
Class 10
-
-
Micro Courses
-
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
