Question

What is the effective resistance between the points A and C for the network shown in the figure?

(A) $ \dfrac{2R}{3} $
(B) $ \dfrac{3R}{2} $
(C) 2R
(D) $ \dfrac{1}{2R} $

Answer 1

Hint: A Wheatstone bridge is an electrical circuit used to measure an unknown electrical resistance by balancing two legs of a bridge circuit, one leg of which includes the unknown component. The primary benefit of the circuit is its ability to provide extremely accurate measurements.
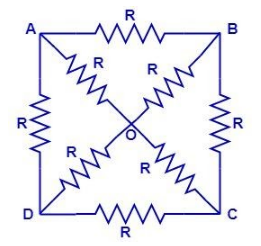
Distinguish the formed Wheatstone bridges in the given circuit which are balanced and hence eradicate the resistances through which no current flows. Then calculate the net resistance through A and C from the new resolved circuit.

Complete step by step solution:
Let us name all the resistors from 1 to 8 as:

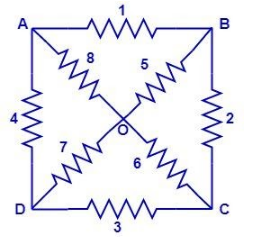
Where $ {{R}_{1}}={{R}_{2}}={{R}_{3}}=.........={{R}_{8}}=R $
Here we can see that
 $ \dfrac{{{R}_{8}}}{{{R}_{4}}}=\dfrac{{{R}_{6}}}{{{R}_{3}}}=1 $
Also,
 $ \dfrac{{{R}_{1}}}{{{R}_{8}}}=\dfrac{{{R}_{2}}}{{{R}_{6}}}=1 $
So AOCD and AOCB form the balanced Wheatstone bridges.
This means that $ {{R}_{5}} $ and $ {{R}_{7}} $ have no flow of current through them and hence provide no resistance in the circuit.
The new circuit becomes:

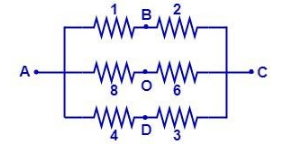
In this new circuit we can clearly see that $ {{R}_{1}} $ and $ {{R}_{2}} $ , $ {{R}_{3}} $ and $ {{R}_{4}} $ , $ {{R}_{6}} $ and $ {{R}_{8}} $ are in series and their resultants are parallel to each other. This final resultant gives us the total resistance required between points A and C.
Now doing the calculations:
 $ \begin{align}
  & R'={{R}_{1}}+{{R}_{2}} \\
 & =R+R \\
 & =2R \\
 & R''={{R}_{3}}+{{R}_{4}} \\
 & =R+R \\
 & =2R \\
 & R'''={{R}_{6}}+{{R}_{8}} \\
 & =R+R \\
 & =2R \\
\end{align} $
Now,
 $ \begin{align}
  & \dfrac{1}{{{R}_{AC}}}=\dfrac{1}{R'}+\dfrac{1}{R''}+\dfrac{1}{R'''} \\
 & =\dfrac{1}{2R}+\dfrac{1}{2R}+\dfrac{1}{2R} \\
 & \dfrac{1}{{{R}_{AC}}}=\dfrac{3}{2R} \\
\end{align} $
Or
 $ {{R}_{AC}}=\dfrac{2R}{3} $
Therefore, option (A) is the correct answer.

Note:
Balanced Wheatstone bridges are used to resolve a complicated circuit of resistors into a simpler form to calculate the net resistance, voltage or current between two points. The Wheatstone bridge is used for measuring the very low resistance values precisely. Wheatstone bridge along with an operational amplifier is used to measure the physical parameters like temperature, strain, light, etc.