Question

Draw a rough sketch of the graph of the function $y = 2\sqrt {1 - {x^2}} ,x \in \left[ {0,1} \right]$ and evaluate the area enclosed between the curve and the x-axis.

Answer 1

Hint: To solve this question, we will use the concept of application of integration. If the curve $y = f\left( x \right)$ lies above the x-axis on interval $\left[ {a,b} \right]$, then the area bounded by the curve $y = f\left( x \right)$, x-axis and the ordinates x = a and x = b is given by,
 \[\int\limits_a^b {\left| {f\left( x \right)} \right|} dx = \int\limits_a^b {f\left( x \right)} dx = \int\limits_a^b y dx\] $\left[ {\therefore f\left( x \right) \geqslant 0{\text{ for all }}x \in \left[ {a,b} \right]\therefore \left| {f\left( x \right)} \right| = f\left( x \right)} \right]$

Complete step-by-step answer:
          

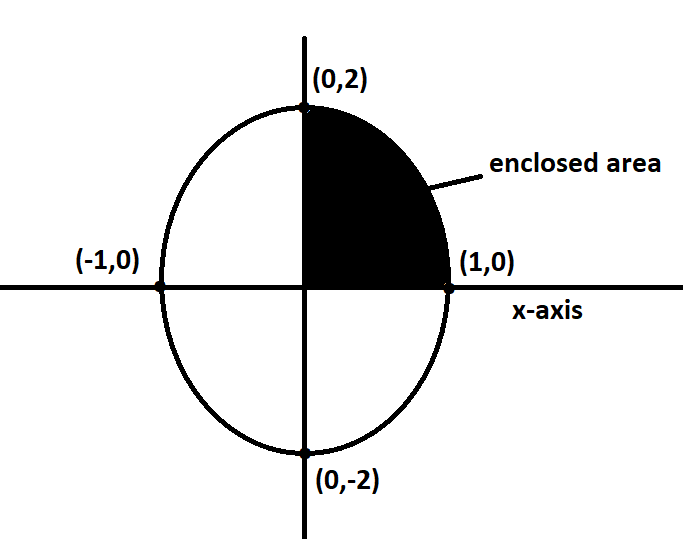
Given that,
$y = 2\sqrt {1 - {x^2}} ,x \in \left[ {0,1} \right]$
Let us simplify this equation of curve in a simple form,
$ \Rightarrow y = 2\sqrt {1 - {x^2}} $ ……. (i)
Squaring both sides on equation (i),
$ \Rightarrow {y^2} = 4\left( {1 - {x^2}} \right)$
\[ \Rightarrow \dfrac{{{y^2}}}{4} = 1 - {x^2}\]
\[ \Rightarrow \dfrac{{{x^2}}}{1} + \dfrac{{{y^2}}}{4} = 1\]
Here, we can see that this is the equation of an ellipse.
So,
$ \Rightarrow y = 2\sqrt {1 - {x^2}} $ will represent the portion of the ellipse lying in the first quadrant.
So, the required area A enclosed between the curve and the x-axis is given by,
\[ \Rightarrow A = \int\limits_0^1 y dx\]
Putting the value of y,
\[ \Rightarrow A = \int\limits_0^1 {2\sqrt {1 - {x^2}} } dx\] ……… (ii)
As we know that,
\[\int {\sqrt {{a^2} - {x^2}} } dx = \dfrac{1}{2}x\sqrt {{a^2} - {x^2}} + \dfrac{{{a^2}}}{2}{\sin ^{ - 1}}\dfrac{x}{a} + C\]
If we compare $\sqrt {{a^2} - {x^2}} $ with \[\sqrt {1 - {x^2}} \],
We get a = 1.
So, the integration of equation (ii) will become,
\[ \Rightarrow A = 2\left[ {\dfrac{1}{2}x\sqrt {1 - {x^2}} + \dfrac{1}{2}{{\sin }^{ - 1}}\dfrac{x}{1}} \right]_0^1\]
\[ \Rightarrow A = 2\left[ {\left( {\dfrac{1}{2}\left( 1 \right)\sqrt {1 - {1^2}} + \dfrac{1}{2}{{\sin }^{ - 1}}\dfrac{1}{1}} \right) - \left( {\dfrac{1}{2}0\sqrt {1 - {0^2}} + \dfrac{1}{2}{{\sin }^{ - 1}}\dfrac{0}{1}} \right)} \right]\]
\[ \Rightarrow A = 2\left[ {\left( {0 + \dfrac{1}{2}\left( {\dfrac{\pi }{2}} \right)} \right) - 0} \right]\]
\[ \Rightarrow A = 2 \times \dfrac{\pi }{4}\]
\[ \Rightarrow A = \dfrac{\pi }{2}\]sq. units.
Hence, the area enclosed between the curve and the x-axis will be \[\dfrac{\pi }{2}\] sq. units.

Note: Whenever we asked such type of questions, we should also remember that, If the curve $y = f\left( x \right)$ lies below the x-axis on interval $\left[ {a,b} \right]$, then the area bounded by the curve $y = f\left( x \right)$, x-axis and the ordinates x = a and x = b is given by,
 \[\int\limits_a^b {\left| {f\left( x \right)} \right|} dx = - \int\limits_a^b {f\left( x \right)} dx = - \int\limits_a^b y dx\] $\left[ {\therefore f\left( x \right) \leqslant 0{\text{ for all }}x \in \left[ {a,b} \right]\therefore \left| {f\left( x \right)} \right| = - f\left( x \right)} \right]$