Question

Distinguish between Myopia and Hypermetropia.

Answer 1

Hint: These are common defects of vision which are due to the elongation and contraction of an eyeball due to which image is not formed on the retina but inside and outside causing malfunctioning of an eye.

Complete step by step answer:
Eye has a powerful lens which can adjust itself to produce proper real image on light sensing retina. The retina contains rods and cones which sense light intensity and colour, respectively, and transmit electrical signals via the optic nerve to the brain which finally processes this information.

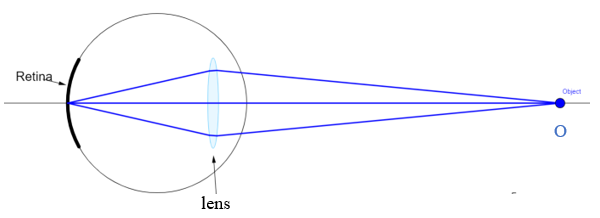
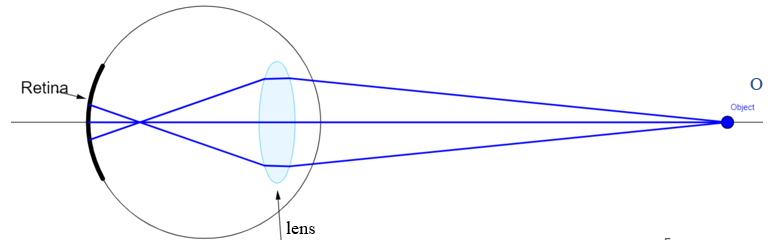
                                                 Normal Image Formation

Myopia – It is a short sightedness where the eye can see only nearer objects and far distance objects are not visible.
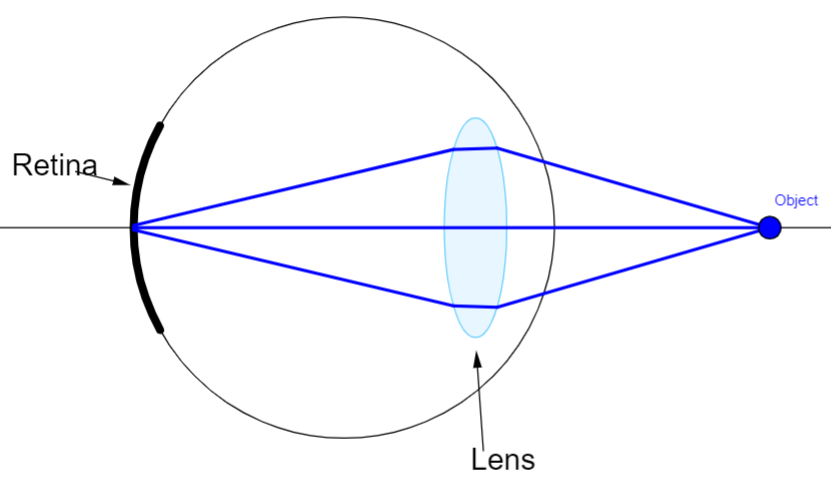
In this case distant objects are not visible because of the elongated eyeball due to which distant object images are formed before the retina.

This can be corrected by using a concave lens which diverges the light ray to make it fall on the retina so that proper image is produced.
Formula for calculating power of concave lens to correct myopia is:
$P=\dfrac{1}{f}=\left[ \dfrac{1}{v}-\dfrac{1}{u} \right]$
Hypermetropia: It is long sightedness where the eye can see only distant objects are nearer objects are not visible. This is because of the contracted eyeball due to which image is not formed on the retina but behind the retina.
 

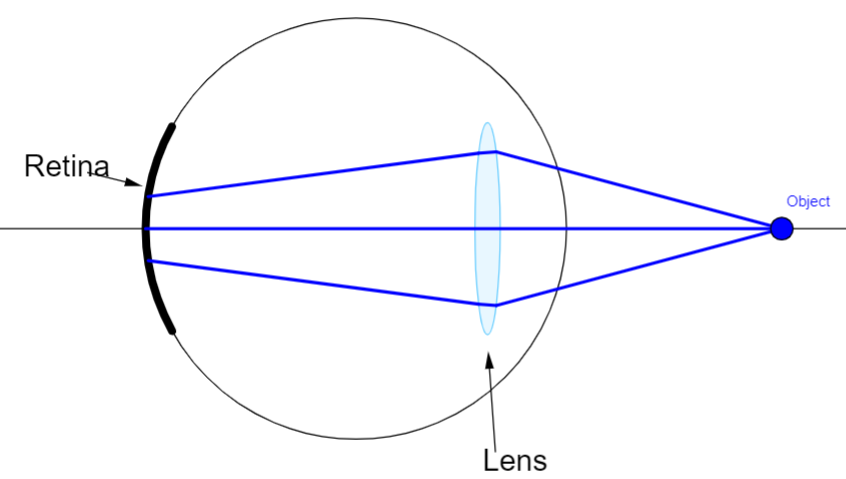
This can be corrected by using a convex lens which is a converging lens and converges the ray towards the retina making the image form on the retina.
Formula for calculating power of concave lens to correct hypermetropia is:
$P=\dfrac{1}{f}=\left[ \dfrac{1}{v}-\dfrac{1}{u} \right]$

Note:
In case of myopia if the object is at infinity then,
$P=\dfrac{1}{f}=-\dfrac{1}{u}$
Power is measured in dioptre (D).
Presbyopia is another type of defect where both near and far objects are not clearly visible. This can be corrected using bifocal length.