Question

Determine the current in each branch of the network shown in the figure.

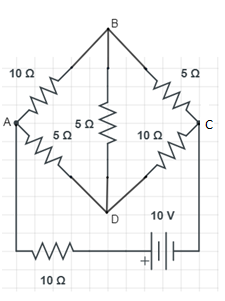
Answer 1

Hint: In order to solve this question first we have to check if this circuit is balanced Wheatstone bridge or unbalanced if it its balanced we can find current in the circuit using Wheatstone bridge formula but if it is unbalanced we have to approach with Kirchhoff’s first law or current law.

Formula used:
Wheatstone bridge formula for checking balanced Wheatstone bridge.
$\Rightarrow \dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{{{R}_{3}}}{{{R}_{4}}}=1$

Complete answer:
Let us draw circuit that is given in the question,

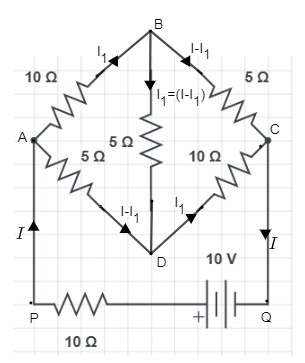
First we will check that the Wheatstone bridge is balanced or not
$\begin{align}
  & \Rightarrow \dfrac{{{R}_{1}}}{{{R}_{2}}}=\dfrac{{{R}_{3}}}{{{R}_{4}}} \\
 & \Rightarrow \dfrac{10}{5}=\dfrac{5}{10} \\
 & \Rightarrow 2=\dfrac{1}{2}......\left( 1 \right) \\
\end{align}$
So from equation (1) we can say that Wheatstone bridge is unbalanced hence current flowing in$5\Omega $resistance between AD is not equal to zero.
Now applying Kirchhoff’s first law in ABDA as show in the figure, now the total current coming is $I$ then the current flow from the AB is ${{I}_{1}}$ and from AD is $I-{{I}_{1}}$
And current from B to D is
$\begin{align}
  & \Rightarrow {{I}_{1}}-\left( I-{{I}_{1}} \right) \\
 & \Rightarrow 2{{I}_{1}}-I \\
\end{align}$
Now according to Kirchhoff’s first law, and from the figure and circuit ABDA as shown in figure
$\begin{align}
  & \Rightarrow 10{{I}_{1}}+5\left( 2{{I}_{1}}-I \right)-5\left( I-{{I}_{1}} \right)=0 \\
 & \Rightarrow 10{{I}_{1}}+10{{I}_{1}}-5I-5I+5{{I}_{1}}=0 \\
 & \Rightarrow 25{{I}_{1}}-10I=0 \\
 & \Rightarrow 25{{I}_{1}}=10I \\
 & \therefore {{I}_{1}}=\dfrac{2}{5}I.......\left( 2 \right) \\
\end{align}$
Now as to consider voltage and outside resistance $10\Omega $ we will apply Kirchhoff’s first law to circuit QPADCQ as shown in figure.
$\begin{align}
  & \Rightarrow 10=10I+5\left( I-{{I}_{1}} \right)+10{{I}_{1}} \\
 & \Rightarrow 10=10I+5I-5{{I}_{1}}+10{{I}_{1}} \\
 & \therefore 10=15I+5{{I}_{1}}......\left( 3 \right) \\
\end{align}$
Now substitute value of equation (2) in equation (3)
$\begin{align}
  & \Rightarrow 10=15I+5\left( \dfrac{2}{5} \right)I \\
 & \Rightarrow 10=15I+2I \\
 & \Rightarrow 10=17I \\
 & \therefore I=\dfrac{10}{17}A......\left( 4 \right) \\
\end{align}$
Now substitute value of equation (4) in equation (2)
$\begin{align}
  & \Rightarrow {{I}_{1}}=\dfrac{2}{5}\left( \dfrac{10}{17} \right) \\
 & \Rightarrow {{I}_{1}}=\dfrac{4}{17}A \\
\end{align}$
Now current in branch AB and CD is
$\Rightarrow {{I}_{1}}=\dfrac{4}{17}A$
Current in branch AD and BC
$\begin{align}
  & \Rightarrow I-{{I}_{1}}=\dfrac{10}{17}-\dfrac{4}{17} \\
 & =\dfrac{6}{17}A \\
\end{align}$
Current in branch BD is
$\begin{align}
  & \therefore 2{{I}_{1}}-I=2\left( \dfrac{4}{17} \right)-\dfrac{10}{17} \\
 & \therefore -\dfrac{2}{17}A \\
\end{align}$
Here negative direction shows that current direction is D to B

Note:
When we are distributing current and resistance that are shown in circuit are equal then current flow will be same in that equal resistance for example circuit AB and CD will have equal current distribution.