Question

Describe the Jahn Teller effect.

Answer 1

Hint: Jahn Teller effect is related to the distortion of a non linear molecular system. It explains the reduction in the symmetry and the energy of the system. Jahn Teller effect is due to the different extent of interactions of ligands with d orbitals of metals.

Complete answer:
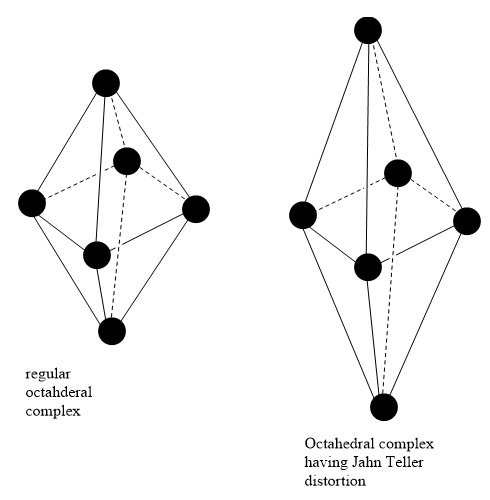
A non linear molecular system undergoes distortion. Due to this distortion, the symmetry and the energy of the system is reduced. This distortion is known as the Jahn Teller effect.
Octahedral complexes can have axial bond lengths different from equatorial bond lengths. Such complexes show the John Teller effect. Axial bond lengths can be greater than equatorial bond lengths. It is also possible that Axial bond lengths can be smaller than equatorial bond lengths. Tetrahedral complexes also show the Jahn Teller effect. This effect depends on the electronic state of the system.
Consider a nonlinear complex. If the electronic configuration in the ground state has degenerate orbitals, then, the complex will remove the degeneracy by distortion so as to achieve lower energy.
In the presence of an octahedral field, d orbitals of metal split into two levels, \[{t_{2g}}\] and \[{e_g}\]. \[{t_{2g}}\] has lower energy and is directed in between the axis so that it does not face the approaching ligands directly. \[{e_g}\] has higher energy and is directed along the axis so that it faces the approaching ligands directly.
The interaction between ligands and \[{e_g}\] orbitals is greater than that between ligands and \[{t_{2g}}\] orbitals, high spin \[{d^4}\], low spin \[{d^7}\] and \[{d^9}\] configurations have greater Jahn Teller effect.

Note: In high spin \[{d^4}\] octahedral complexes of \[{\text{C}}{{\text{r}}^{{\text{2 + }}}}{\text{ and C}}{{\text{u}}^{{\text{2 + }}}}\], Jahn Teller effect is observed as the lone pair of electrons split degenerate \[{e_g}\] level into \[{d_{{z^2}}}{\text{ }} and {\text{ }}{d_{{x^2} - {y^2}}}\] orbital.