Question

Derive an expression for maximum speed of a car on a banked road in circular motion.

Answer 1

Hint:In this question, we need to find the maximum speed of the car at which car doesn’t skid while moving in a circular banked road. We basically balance all the factors of the forces exerted on a car in x-axis direction and y-axis direction.
To solve any balancing problems, whether motion is translational or rotational, we always balance forces acting along x-axis and y-axis.
In case of rotational motion, we balance torques acting on the body.

Complete step-by-step answer:
Several formulas used in our calculations are-
Gravitational attraction force – mg
Frictional force (f) – acting between car’s tire and road, and parallel to the slope of road
Normal force (N)- It is a reaction force of the gravitational force exerted by the road on car
Centripetal force $\left( \dfrac{m{{v}^{2}}}{r} \right)$ - acting towards the center of the circular path followed by the car.

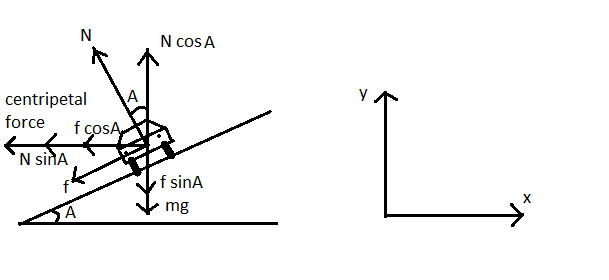
Let’s take inclination angle A of road with respect to the x-axis as shown in the above diagram. Now we can balance all the x-axis and y-axis factors of forces. Refer to the figure.
(1) Balancing all the forces acting along the x-axis-
$f\cos (A)+N\sin (A)=\dfrac{m{{v}^{2}}}{r}$
Substituting the value $f=\mu N$ into equation, we get
$\begin{align}
  & \mu N\cos (A)+N\sin (A)=\dfrac{m{{v}^{2}}}{r} \\
 & \Rightarrow N\left( \mu \cos A+\sin A \right)=\dfrac{m{{v}^{2}}}{r}......(1) \\
\end{align}$
(2) Balancing all the forces acting along the y-axis-
$\begin{align}
  & N\cos A=f\sin A+mg \\
 & \Rightarrow N\cos A=\mu N\sin A+mg \\
 & \Rightarrow N\left( \cos A-\mu \sin A \right)=mg........(2) \\
\end{align}$
(3) Frictional force-
$f=\mu N$
Now we will use these three equations to find the value of speed (v).
Now we can divide equation (1) and (2), we get
\[\begin{align}
  & \dfrac{{{v}^{2}}}{rg}=\dfrac{\left( \mu +\tan A \right)}{\left( 1-\mu \tan A \right)} \\
 & \Rightarrow v=\sqrt{\dfrac{rg\left( \mu +\tan A \right)}{\left( 1-\mu \tan A \right)}} \\
\end{align}\]
This is an expression for maximum speed of a car on a banked road in circular motion.

Note: (1) Roads are banked to prevent high speed cars from skidding.
(2) If a car is moving at a speed more than mentioned above, it will skid.
(3) If the force of friction is not strong enough, the vehicle will skid. Also, note that friction acts downwards along the road, as the tendency of the car is to skid up.