Question

Define the bijective function.

Answer 1

Hint: (The Function which is One-one and onto are bijective)
Let say a function is present there ‘$f$’ That function $f$ is said to bijective if it is one-one and onto. First, we write the definite of one-one function and onto function then define the difference between them to get a suitable answer.

Complete step-by-step solution:
One-One Function - One to one function basically denotes the mapping of two sets. A function $g\,\,$is one-to-one if every element of the range of $g$ corresponds to exactly one element of the domain of $g$. One-to-one is also written as 1-1. A function $f()$ is a method, which relates elements/values of one variable to the elements/values of another variable, in such a way that elements of the second variable are identically determined by the elements of the first variable.

Above shown is the Venn diagram of a one-one function in which every element of the domain is related to the single element in the codomain. this can be onto as well as every element is related. So we can say the above function in the Venn diagram is bijective. Since it is both one-one and onto.
Onto Function - Onto function could be explained by considering two sets, Set A and Set B which consist of elements. If for every element of B there is at least one or more than one element matching with A, then the function is said to be onto function.

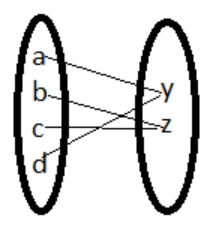
The above diagram is of onto function since every element of the domain is related to a single element in the codomain. It is not one-one since the two elements of the domain set are related to a single element of codomain set.


Note: We have to keep in mind that, One-One function is also called injective function and Onto function is also called bijective function. Hence most of the questions use these terms.