Question

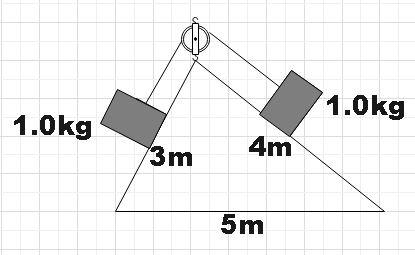
Consider the situation shown in the figure. All the surfaces are frictionless and the string and the pulley are light. Find the magnitude of the acceleration of the two blocks.

A.$g$
B.$\dfrac{2g}{3}$
C.$\dfrac{g}{5}$
D.$\dfrac{g}{10}$

Answer 1

Hint: Firstly you could find the sine of the two angles in the given system. Then you could consider the given two blocks separately and make a free body diagram for each of them. After that, you could balance the forces in the system and then substitute the above relation. This followed by necessary rearrangements will give the answer.

Complete Step by step solution:
In the question, we are given a pulley mass system with frictionless surface and light pulley and string. We are supposed to find the magnitude of acceleration of the blocks.

As these blocks are connected at the ends of the same string, both of them will have the same acceleration.

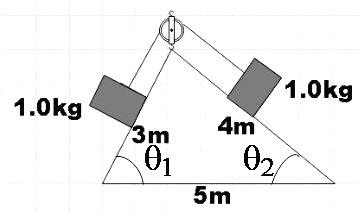
From this figure, we see that,
$\sin {{\theta }_{1}}=\dfrac{4}{5}$ ……………………………………. (1)
$\sin {{\theta }_{2}}=\dfrac{3}{5}$ ……………………………………. (2)

Now let us make the free body diagram of the blocks marking all the force acting on them.

Now we could balance the forces acting on the block to get,
$mg\sin {{\theta }_{1}}-T=ma$ ……………………………………. (3)

Now, balancing the forces on the other block we get,
$T-mg\sin {{\theta }_{2}}=ma$ ……………………………………. (4)

Adding (3) and (4), we get,
$mg\sin {{\theta }_{1}}-mg\sin {{\theta }_{2}}=2ma$
$\Rightarrow mg\left( \sin {{\theta }_{1}}-\sin {{\theta }_{2}} \right)=2ma$
Substituting (1) and (2), we get,
$mg\left( \dfrac{4}{5}-\dfrac{3}{5} \right)=2ma$
$\Rightarrow 2a=\dfrac{g}{5}$
$\therefore a=\dfrac{g}{10}$

Therefore, we found the magnitude of acceleration of the block to be,
$a=\dfrac{g}{10}$

Hence, we found option D to be the correct answer.

Note:
In the question, we have considered that the mass on the right side is accelerating upwards and the one on the other side is accelerating downwards. We have used this direction while making the equations (3) and (4) by balancing the forces. We have taken tension in the string to be greater than the sine component of weight on the right side and the opposite condition for the other side.