Question

Consider the decay of a free neutron at rest: $n \to p + {e^ - }$ .
Show that the two-body decay of this type must necessarily give an electron of fixed energy and, therefore, cannot for the observed continuous energy distribution in the $\beta $-decay of a neutron or a nucleus.

Answer 1

Hint: According to conservation of linear momentum, the initial linear momentum of the system is always equal to final linear momentum. Also, the energy of the system should also remain conserved as per the law of conservation of energy.

Complete step by step answer:
Given: Neutron particle decays into two particles: a proton and an electron.
The formula to calculate the initial momentum of neutron is
$ {p_i} = {m_n}{v_i}$
Here, ${p_i}$ is the initial momentum, ${m_n}$ is the mass of the neutron and ${v_i}$ is the initial velocity.
Initially the neutron is at rest therefore the initial velocity of the neutron is zero.
Substitute$0$for ${v_i}$ in the formula to calculate the initial momentum of the neutron.
$\begin{array}{c}
{p_i} = {m_n}\left( 0 \right)\\
 = 0
\end{array}$
The formula to calculate the final momentum of the decay particles is
${p_f} = {m_p}{v_p} + {m_e}{v_e} $
Here, ${p_f}$ is the final momentum,${m_p}$ is the mass of proton, ${v_p}$ is the velocity of proton, ${m_e}$ is the mass of electron and ${v_e}$ is the velocity of electron.
According to conservation of linear momentum,
${p_i} = {p_f} $
Substitute $0$ for ${p_i}$ and ${m_p}{v_p} + {m_e}{v_e}$ for ${p_f}$ in the conservation of energy and solve to obtain the formula for velocity of proton.
$ 0 = {m_p}{v_p} + {m_e}{v_e}\\$
$\implies {m_p}{v_p} = - {m_e}{v_e}\\$
$\implies {v_p} = - \dfrac{{{m_e}{v_e}}}{{{m_p}}}$
This negative sign in the value of velocity shows that the proton and electron moves in the opposite direction with respect to each other.
Initially as the neutron is at rest, it means the neutron possesses some rest mass energy. The formula to calculate the rest mass energy of the neutron is
${E_n} = \Delta m{c^2}$
Here, ${E_n}$ is the rest mass energy of the neutron, $\Delta m$ is the mass converted into energy and $c$ is the speed of light.
After the decay, both the particles possess kinetic energy. The formula to calculate the total energy of the system after decay is
${E_f} = \dfrac{1}{2}{m_e}v_e^2 + \dfrac{1}{2}{m_p}v_p^2$
Here, ${E_f}$ is the final energy of the system.
According to conservation of energy,
${E_n} = {E_f}$
Substitute $\Delta m{c^2}$ for${E_n}$ and$\dfrac{1}{2}{m_e}v_e^2 + \dfrac{1}{2}{m_p}v_p^2$ for ${E_f}$ in the conservation of energy.
$\Delta m{c^2} = \dfrac{1}{2}{m_e}v_e^2 + \dfrac{1}{2}{m_p}v_p^2$
Substitute$ - \dfrac{{{m_e}{v_e}}}{{{m_p}}}$ for${v_p}$ in the above equation and solve to calculate the velocity of the electron.
$ \Delta m{c^2} = \dfrac{1}{2}{m_e}v_e^2 + \dfrac{1}{2}{m_p}{\left( { - \dfrac{{{m_e}{v_e}}}{{{m_p}}}} \right)^2}\\$
$\implies \Delta m{c^2} = \dfrac{1}{2}{m_e}v_e^2 + \dfrac{1}{2}\dfrac{{m_e^2v_e^2}}{{{m_p}}}\\$
$\implies \dfrac{{v_e^2}}{2}{m_e}\left( {1 + \dfrac{{{m_e}}}{{{m_p}}}} \right) = \Delta m{c^2}\\$
$\therefore v_e^2 = \dfrac{{2\Delta m{c^2}}}{{{m_e}\left( {1 + \dfrac{{{m_e}}}{{{m_p}}}} \right)}}$
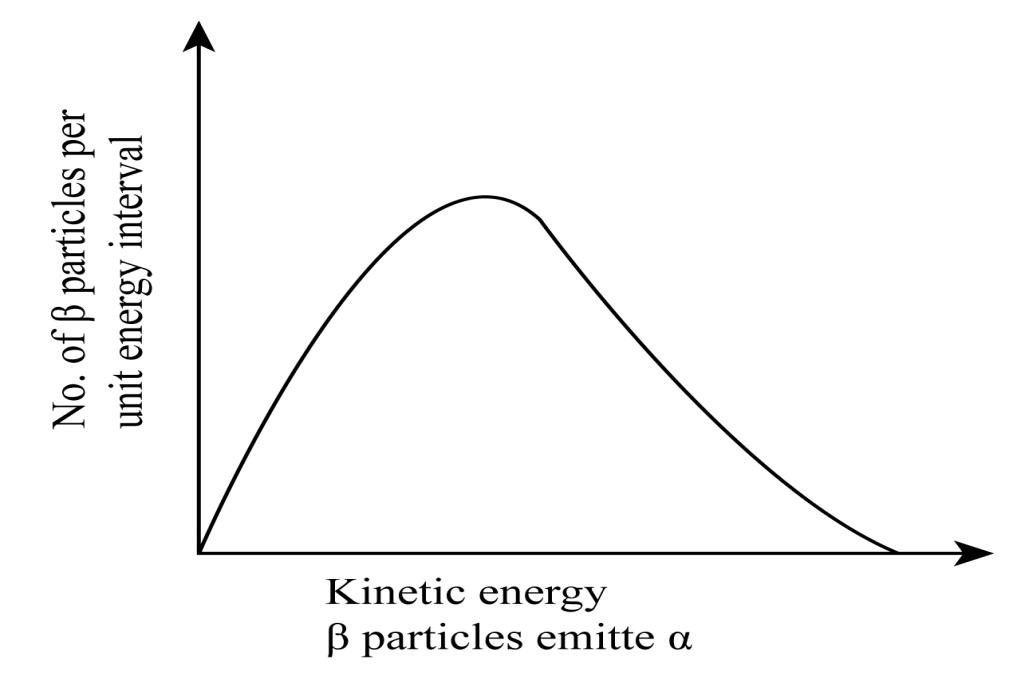
This shows that the velocity of the electron is always a fixed value; therefore the energy of the electron should be a fixed value. This is the reason why a continuous energy distribution cannot be observed.

Note:
 The simple result for this exercise was one among the several arguments advanced by W.Pauli to predict the existence of a third particle in the decay products of $\beta $-decay. This particle is known as neutrino. We now know that it is a particle of intrinsic spin ½ (like p, e or n), but is neutral, and either massless or having an extremely small mass (compared to the mass of an electron) and which interacts very weakly with matter. The correct decay process of the neutron is: $n \to p + {e^ - } + v$ ]