
Charge ${{Q}_{1}}$ and ${{Q}_{2}}$ lie inside and outside respectively of a closed surface S. Let E be the field at any point on S and $\phi $ be the flux of E over S. Choose the incorrect statement.
A. If ${{Q}_{1}}$ changes, both E and $\phi $ will change.
B. If ${{Q}_{2}}$ changes, E will change but $\phi $will not change.
C. If ${{Q}_{1}}=0$ and ${{Q}_{2}}\ne 0$then $E\ne 0$ but $\phi =0$.
D. If ${{Q}_{1}}\ne 0$ and ${{Q}_{2}}=0$then $E=0$ but $\phi \ne 0$
Answer
504k+ views
Hint: As a first step, one could read the question well. Then you could recall as to how we find the electric field at a particular point and also the electric flux at that point. After that you could get help from Gauss's law to arrive at a conclusion for each of the given statements.
Formula used:
Gauss’s law,
$\phi =\dfrac{{{q}_{enclosed}}}{{{\varepsilon }_{0}}}$
Complete step-by-step solution:
In the question, we are given two charges located inside and outside of a closed sphere S. We are also said that E is the electric field on point S and $\phi $ is the flux of E on S. We are supposed to find the correct statements among the given ones.
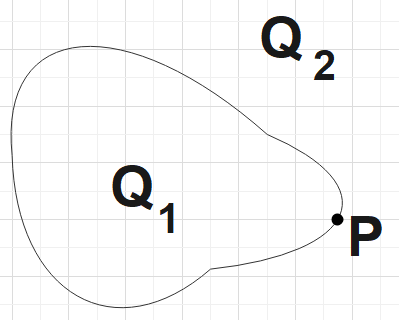
The point to be kept in mind is that, electric field at any point would be due to all of the charges in the point’s vicinity be it outside or inside. Now for the electric flux at a point, the charge enclosed by the closed surface would solely be responsible for it. From Gauss’s law, we know that, electric flux,
$\phi =\dfrac{{{q}_{enclosed}}}{{{\varepsilon }_{0}}}$
Here, the charge enclosed by the closed surface is ${{Q}_{1}}$.
For option A, it is true as the change in ${{Q}_{1}}$ would cause change in the values of E as well as $\phi $.
For option B, it is also true as ${{Q}_{2}}$ is not enclosed by the surface and wouldn't affect the flux but only the electric field.
For the option C, it is also true, as the enclosed charge being zero will only cause the flux to be zero. However the electric field would still not be zero as there is another charge present.
Option D is a false statement. Electric field wouldn’t be zero as there would be the field due to charge ${{Q}_{1}}$ at the point.
Hence, option D is the incorrect statement.
Note: For any questions involving finding the false statement from the given ones, one should deal with it in a step by step manner. You should consider each statement one by one and justify whether they are true or false. Thus we could arrive at a conclusion avoiding further confusions.
Formula used:
Gauss’s law,
$\phi =\dfrac{{{q}_{enclosed}}}{{{\varepsilon }_{0}}}$
Complete step-by-step solution:
In the question, we are given two charges located inside and outside of a closed sphere S. We are also said that E is the electric field on point S and $\phi $ is the flux of E on S. We are supposed to find the correct statements among the given ones.
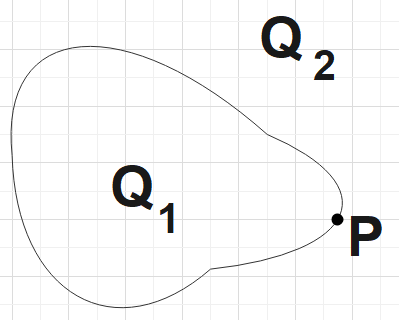
The point to be kept in mind is that, electric field at any point would be due to all of the charges in the point’s vicinity be it outside or inside. Now for the electric flux at a point, the charge enclosed by the closed surface would solely be responsible for it. From Gauss’s law, we know that, electric flux,
$\phi =\dfrac{{{q}_{enclosed}}}{{{\varepsilon }_{0}}}$
Here, the charge enclosed by the closed surface is ${{Q}_{1}}$.
For option A, it is true as the change in ${{Q}_{1}}$ would cause change in the values of E as well as $\phi $.
For option B, it is also true as ${{Q}_{2}}$ is not enclosed by the surface and wouldn't affect the flux but only the electric field.
For the option C, it is also true, as the enclosed charge being zero will only cause the flux to be zero. However the electric field would still not be zero as there is another charge present.
Option D is a false statement. Electric field wouldn’t be zero as there would be the field due to charge ${{Q}_{1}}$ at the point.
Hence, option D is the incorrect statement.
Note: For any questions involving finding the false statement from the given ones, one should deal with it in a step by step manner. You should consider each statement one by one and justify whether they are true or false. Thus we could arrive at a conclusion avoiding further confusions.
Recently Updated Pages
A man running at a speed 5 ms is viewed in the side class 12 physics CBSE

The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

State and explain Hardy Weinbergs Principle class 12 biology CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Which of the following statements is wrong a Amnion class 12 biology CBSE

Differentiate between action potential and resting class 12 biology CBSE

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE




