Question

An α−particle and a proton moving with the same speed enter the same magnetic field region at right angles to the direction of the field. Show the trajectories followed by the two particles in the region of the magnetic field. Find the ratio of the radii of the circular paths which the two particles may describe,

Answer 1

Hint:Here we have two charged particles one is proton and the other is an alpha particle and they both are moving in a straight line towards the positive x-axis. They enter a region of magnetic field perpendicularly and we need to fight the trajectory since they both are charged they will be acted upon by the magnetic force

Complete step by step answer:
The magnetic force on a charged particle placed in a magnetic field is given by \[\overrightarrow{F}=q(\overrightarrow{v}\times \overrightarrow{B})\]
The angle between the velocity vector and the magnetic field is \[90{}^\circ \], so the magnitude of the magnetic force will be,
$F=qvB$
The direction is given as \[=v\widehat{i}\times B(-\widehat{k})\].
Since we are interested in finding the direction, taking only unit vectors we get,
\[\begin{align}
& =\widehat{i}\times (-\widehat{k}) \\
& =\widehat{j} \\
\end{align}\]
So the force acts towards the positive y-axis that is in an upward direction for both the particles. Now let us find the magnitude for both of them. Since both have the same velocity and the value of the magnetic field is the same for both, F=qvB,
Force is directly proportional to the magnitude of charge and the charge on the alpha particle is twice the value of charge on the proton, so the force acting on the alpha particle will be two times in magnitude the force acting on the proton.
So the trajectory looks like,

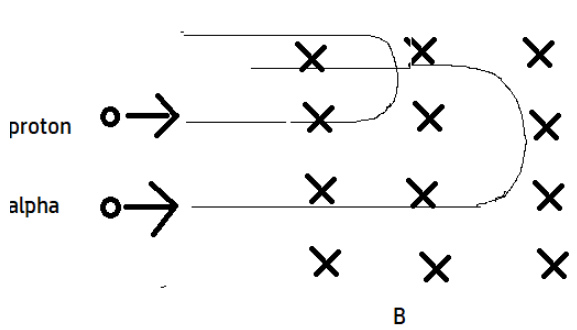
Note:Proton has a charge q and the charge on the alpha particle which is a doubly ionized helium atom is 2q. Both are positive and when they enter the magnetic field, they experience the force. If the angle between the velocity vector and the magnetic field was zero, then both of them would have passed undeflected.