Question

An equilateral triangle of side $a$ carries a current $I$ . Find the magnetic field at P which is the vertex of the triangle.
A) $\dfrac{{{\mu _0}I}}{{2\sqrt 3 \pi a}} \odot $

B) $\dfrac{{{\mu _0}I}}{{2\sqrt 3 \pi a}} \otimes $
C) $\dfrac{9}{2}\left( {\dfrac{{{\mu _0}I}}{{\pi a}}} \right) \odot $
D) $\dfrac{9}{2}\left( {\dfrac{{{\mu _0}I}}{{\pi a}}} \right) \otimes $

Answer 1

Hint: From the given figure, we deduct that the magnetic field at P will be only due to the base of the triangle. The other two sides will not contribute. Biot-Savart’s law will give the magnitude of this magnetic field to be proportional to the current along the base and inversely proportional to the distance from the base to point P. The right-hand thumb rule gives the direction of the magnetic field to be along the direction in which the fingers curl around the right thumb which represents the direction of the current.

Formula used:
-The magnitude of the magnetic field given by Biot-Savart’ law at a point from a current-carrying wire is given by, $B = \dfrac{{{\mu _0}}}{{4\pi }}\left( {\dfrac{I}{d}} \right)\sin \theta $ where $I$ is the current in the wire, $d$ is the distance from the wire to the point and $\theta $ is the angle subtended at that point.

Complete step by step answer.
Step 1: Sketch the triangle representing the distance from the base and the angle made at P.

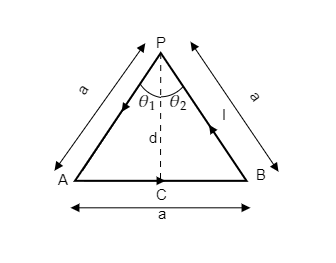
In the above figure, we have the equilateral triangle.
The distance from the base of the triangle is represented by the dotted line PC and it is denoted by $d$. PC is a perpendicular bisector to the base of the triangle PAB.
The corresponding angles made by P with respect to the base are marked as ${\theta _1}$ and ${\theta _2}$ .
Step 2: Using the Pythagoras theorem, express the distance PC.
Consider the right triangle PCB as given below.

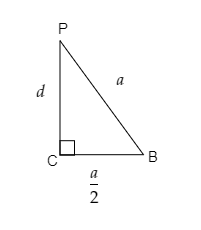
We have $CB = \dfrac{a}{2}$ and $PB = a$ .
Then the distance from the base to point P given by Pythagoras theorem will be $d = \sqrt {{a^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} $
$ \Rightarrow d = \sqrt {\dfrac{{3{a^2}}}{4}} = \dfrac{{\sqrt 3 a}}{2}$
Thus we have $d = \dfrac{{\sqrt 3 a}}{2}$ .
Step 3: Express the magnitude of the magnetic field using Biot-Savart’s law.
The magnitude of the magnetic field given by Biot-Savart’ law at P can be expressed as $B = \dfrac{{{\mu _0}}}{{4\pi }}\left( {\dfrac{I}{d}} \right)\left( {\sin {\theta _1} + \sin {\theta _2}} \right)$ --------- (1)
where $I$ is the current along the base, $d$ is the distance from the base to P and ${\theta _1}$ , ${\theta _2}$ are the angles subtended at P by the base.
Substituting for $d = \dfrac{{\sqrt 3 a}}{2}$ and ${\theta _1} = {\theta _2} = 30^\circ $ in equation (1) we get, $B = \dfrac{{{\mu _0}}}{{4\pi }}\left( {\dfrac{{2I}}{{\sqrt 3 a}}} \right)\left( {\sin 30^\circ + \sin 30^\circ } \right)$
We know that $\sin 30^\circ = \dfrac{1}{2}$ .
$ \Rightarrow B = \dfrac{{{\mu _0}I}}{{2\sqrt 3 \pi a}}$
So the magnitude of the magnetic field at P is $B = \dfrac{{{\mu _0}I}}{{2\sqrt 3 \pi a}}$ . Its direction as given by the right-hand thumb rule will be into the plane represented by $ \otimes $ .
So we have $\vec B = \dfrac{{{\mu _0}I}}{{2\sqrt 3 \pi a}} \otimes $
Thus the correct option is B.
Note: The magnetic field due to the side PA and PB are zero as P lies on the vertex of these two lines and as the current is directed opposite in these sides. For an equilateral triangle, each angle is $60^\circ $ . The perpendicular bisector PC bisects the angle P into $30^\circ $ each. Here when we take the direction of the current in the base of the triangle along the right thumb we see that the fingers curl inwards.