Question

An element germanium crystallises in a bcc type structure with an edge of unit cell $288pm$ and the density of the element is $7.2gc{m^{ - 3}}$ . Calculate the number of atoms present in $52g$ of the crystalline element and also calculate the atomic mass of the elements.

Answer 1

Hint:Density of a substance is the amount of matter stored in per unit volume. Amount of matter, which can also be called the total mass of a unit cell, will be the summation of mass of all the germanium atoms in the unit cell. If we know the mass value and mass of one atom, the number of atoms can be derived.
Formula Used:
${a^3} = \dfrac{{z \times M}}{{{N_A} \times \rho }}$
Where:
$\rho = density,z = Number\,of\,atoms\,in\,a\,unit\,cell,M = molar\,mass,{N_A} = Avogadro\,Number,a = unit\,length$

Complete step by step answer:
Let us understand some terms which we will need:
Unit cell: the smallest group of particles in the material that constitutes this repeating pattern is the unit cell of the structure. The unit cell completely reflects the symmetry and structure of the entire crystal, which is built up by repetitive translation of the unit cell along its principal axes.
BCC stands for Body centred cubic close packing and is shown in the diagram below. Hence It consist of net of two atoms.

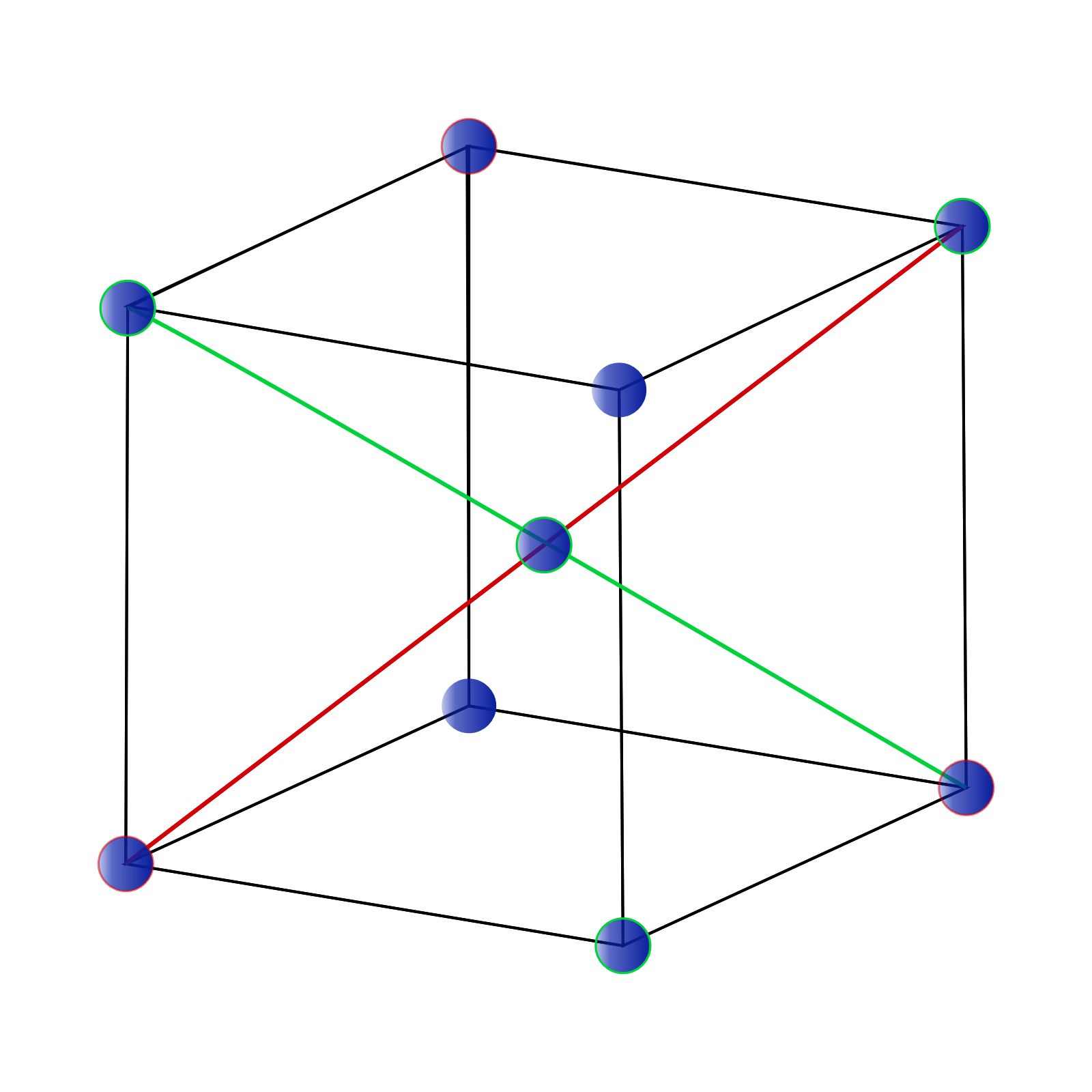
Here, we have $8$ atoms on the corners which are being shared with $8$ unit cell and $1$ atoms in the centre which are not being shared. Therefore One unit cell will have Number of atoms in one BCC unit cell $(Z) = \dfrac{1}{8} \times 8 + 1 \Rightarrow 2$ $Z = 2$ Let us understand the formulae we will be using: We known that Density is the ratio of Mass to Volume and can be written as $Density = \dfrac{{Mass}}{{Volume}}$ We know that: $Mass = 52g,Density = 7.2g{m^{ - 3}}$ Substituting these values in the above equation, we get: $Volume = \dfrac{{52}}{{7.2}} \Rightarrow 7.22$ $Volume = 7.22c{m^3}$ For a cube, the volume can be modified as $Volume = {(unit\,\,length)^3}$ Since, all sides are equal in a cube. $a = 288 \times {10^{ - 10}}c{m^{}}$ We get: $Volume = $ ${(288 \times {10^{ - 10}})^3} \Rightarrow 2.389 \times {10^{ - 23}}$ We can say that number of unit cells can be $ = \dfrac{{Total\,volume}}{{Volume\,of\,one\,unit\,cell}}$ Substituting the above value, we get: $\dfrac{{7.22}}{{2.389 \times {{10}^{ - 23}}}}$ We get the number of unit cells as $3.022 \times {10^{23}}$ We know that one unit cell has two atoms, therefore, $3.022 \times {10^{23}}$ cells will have $3.022 \times {10^{23}} \times 2 \Rightarrow 6.044 \times {10^{23}}$ Number of atoms will be = $6.044 \times {10^{23}}$
Mass can be given as $Mass\,of\,1\,atom = \dfrac{{Molar\,Mass}}{{Avogadro's\,Number}}$ Number of atoms in a unit cell is given by Z and hence mass of the atoms in a unit cell can be given by $Mass\,of\,atoms\,in\,a\,unit\,cell = \dfrac{{Z \times M}}{{{N_A}}}$ Substituting the value of Mass of atom in a unit cell, in the above equation, we get, \[Density = \dfrac{{Z \times Molar\,Mass}}{{{{(unit\,length)}^3} \times {N_A}}}\] which can also be written as $\rho = \dfrac{{Z \times m}}{{{a^3} \times {N_A}}}$ $\rho = density,z = Number\,of\,atoms\,in\,a\,unit\,cell,M = molar\,mass,{N_A} = Avogadro\,Number,a = unit\,length$ From the question, we know the values of $\rho = 7.2gc{m^{ - 3}},a = 288 \times {10^{ - 10}}cm$ and we have calculated that for BCC the value of $Z = 2$ . Substituting these values we get: $mass = \dfrac{{7.2 \times {{(288 \times {{10}^{ - 10}})}^3} \times 6.022 \times {{10}^{23}}}}{2}$ $mass = 51.78gmo{l^ - }$ Hence the $molar\,mass = 51.78gmo{l^ - }$. Number of atoms = $6.044 \times {10^{23}}$

Note:
-The Value for $Z$ changes with different Lattices. The highest Value of $Z$ is $4$ which is in the case of Face centred Cubic lattice and the lowest possible value of $Z$ is $1$ which is in case of Simple cubic lattice.
-Face centred Lattice can be formed in Cubic close Packing and Hexagonal close packing, Although the Value for $Z$ does not change, but the formula to calculate the volume of the hexagon will be different for the volume of a cube.