
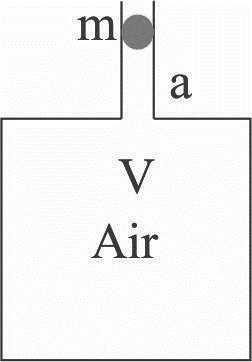
An air chamber having a volume V and a cross-sectional area of the neck is a into which a ball of mass m can move up and down without friction. Show that when the ball is pressed down a little and released, it executes SHM .Obtain an expression for the Time Period of oscillations assuming pressure –volume variations of air to be isothermal.
Answer
232.8k+ views
Hint: In the above given diagram it is given that the system is Isothermal that means the temperature in the whole system is assumed to be constant. Obtain the formula for the restoring force on the ball and the restoring force in simple harmonic motion. Compare both forces to obtain a time period of oscillations.
Complete step by step answer:
Let us consider the volume of the air chamber is $V$
Assume the area of cross-section of the neck is $a$
Also let the value of the Mass of the ball is $m$
The pressure inside the chamber is equal to the atmospheric pressure.
Let the ball be depressed by x units. As a result of this depression, there would be a decrease in the volume and an increase in the pressure inside the chamber.
Decrease in the volume of the air chamber, $\Delta V = ax$
Write the expression for the Bulk modulus of air.
$B = \dfrac{-p}{\dfrac{ax}{V}}$
In this case Stress is the increase in the pressure.
The negative sign indicates that it increases with decrease in Volume.
Now, write the expression for the pressure.
$P = \dfrac{-Bax}{V}$
The restoring force acting on the ball is calculated as,
$F = P \times a = \left( { - Bax/V} \right)\left( a \right) = - B{a^2}x/V$.........…. (i)
We know that in Simple Harmonic Motion, the equation for restoring force is written as
$F = - kx$.........…. (ii)
Where, $k$ is the spring constant.
Comparing equation (i) and (ii) we get,
$ - kx = - \dfrac{{B{a^2}x}}{V}$
$\Rightarrow k = \dfrac{B{a^2}}{V} $
Time period for the equation is,
$T = 2\pi \sqrt {\dfrac{m}{k}} $
Substitute the values of $k$ in the above equation to obtain,
$T = 2\pi \sqrt{\dfrac{mV}{B{a^2}}}$
Note: Do not confuse the negative sign mentioned in the expression. The negative sign indicates decrease in the volume and an increase in the pressure inside the chamber.
Complete step by step answer:
Let us consider the volume of the air chamber is $V$
Assume the area of cross-section of the neck is $a$
Also let the value of the Mass of the ball is $m$
The pressure inside the chamber is equal to the atmospheric pressure.
Let the ball be depressed by x units. As a result of this depression, there would be a decrease in the volume and an increase in the pressure inside the chamber.
Decrease in the volume of the air chamber, $\Delta V = ax$
Write the expression for the Bulk modulus of air.
$B = \dfrac{-p}{\dfrac{ax}{V}}$
In this case Stress is the increase in the pressure.
The negative sign indicates that it increases with decrease in Volume.
Now, write the expression for the pressure.
$P = \dfrac{-Bax}{V}$
The restoring force acting on the ball is calculated as,
$F = P \times a = \left( { - Bax/V} \right)\left( a \right) = - B{a^2}x/V$.........…. (i)
We know that in Simple Harmonic Motion, the equation for restoring force is written as
$F = - kx$.........…. (ii)
Where, $k$ is the spring constant.
Comparing equation (i) and (ii) we get,
$ - kx = - \dfrac{{B{a^2}x}}{V}$
$\Rightarrow k = \dfrac{B{a^2}}{V} $
Time period for the equation is,
$T = 2\pi \sqrt {\dfrac{m}{k}} $
Substitute the values of $k$ in the above equation to obtain,
$T = 2\pi \sqrt{\dfrac{mV}{B{a^2}}}$
Note: Do not confuse the negative sign mentioned in the expression. The negative sign indicates decrease in the volume and an increase in the pressure inside the chamber.
Recently Updated Pages
Dimensions of Charge: Dimensional Formula, Derivation, SI Units & Examples

How to Calculate Moment of Inertia: Step-by-Step Guide & Formulas

Circuit Switching vs Packet Switching: Key Differences Explained

Dimensions of Pressure in Physics: Formula, Derivation & SI Unit

JEE General Topics in Chemistry Important Concepts and Tips

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




