Question

A uniform rod is hinged as shown in the figure given below and is released from a horizontal position. Find the angular velocity of the rod as it passes the vertical position.

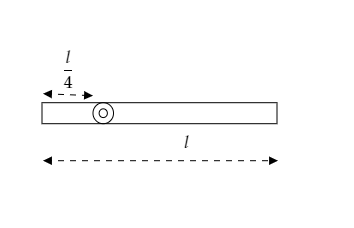
A) $\sqrt {\dfrac{{12g}}{{3l}}} $
B) $\sqrt {\dfrac{{2g}}{{3l}}} $
C) $\sqrt {\dfrac{{24g}}{{7l}}} $
D) $\sqrt {\dfrac{{3g}}{{7l}}} $

Answer 1

Hint:Here, the point of suspension of the rod is at a distance $\dfrac{l}{4}$ from the centre of the rod. So, the moment of inertia of the rod about the hinge can be obtained using the parallel axes theorem. Also, as the rod rotates and reaches the vertical position the total energy of the system must be conserved.

Formulas used:
-The moment of inertia of a uniform rod about an axis passing through its centre is given by, $I = \dfrac{{M{l^2}}}{{12}}$ where $M$ is the mass of the rod and $l$ is its length.
-The rotational kinetic energy of a body with a moment of inertia $I$ and angular velocity $\omega $ is given by, $K = \dfrac{1}{2}I{\omega ^2}$ .
-The potential energy of a body of mass $m$ at a height $h$ from the point of suspension is given by $U = mgh$

Complete step by step answer.
Step 1: Sketch a figure of the setup and list the parameters known.

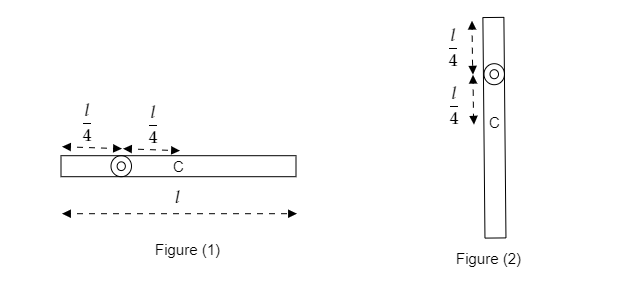
Figure (1) shows the initial horizontal position of the uniform rod of mass $m$ and length $l$ hinged at a distance $\dfrac{l}{4}$ from one of its ends. This rod then rotates about the hinge and reaches the vertical position as shown in figure (2). The centre of mass C of the rod is located at a distance $\dfrac{l}{4}$ from the point of suspension.
Step 2: Using parallel axes theorem, find the moment of inertia of the rod about the hinge.
The moment of inertia of the uniform rod about an axis passing through its centre is given by, $I = \dfrac{{m{l^2}}}{{12}}$ where $m$ is the mass of the rod and $l$ is its length.
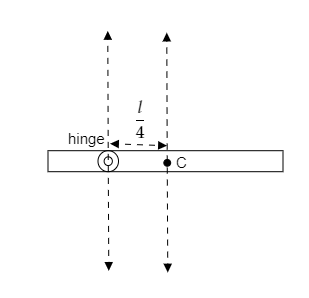
According to the parallel axes theorem, the moment of inertia of the rod about the hinge must be equal to the moment of inertia of the rod about an axis passing through its centre of mass plus the product of its mass and the square of the distance $\dfrac{l}{4}$ between the two axes.

The above figure depicts the parallel axes theorem.

Then the moment of inertia of the rod about the hinge will be $I = \dfrac{{m{l^2}}}{{12}} + m{\left( {\dfrac{l}{4}} \right)^2}$ .
Simplifying we get, $I = \dfrac{{m{l^2}}}{{12}} + {\dfrac{{ml}}{{16}}^2} = \dfrac{{7m{l^2}}}{{48}}$
Thus the moment of inertia of the rod about the hinge is $I = \dfrac{{7m{l^2}}}{{48}}$

Step 3: Using the energy conservation theorem, find the angular velocity of the rod.
According to the conservation of energy, the loss in the potential energy of the rod constitutes the gain in the kinetic energy of the rod.
The potential energy of the rod will be $U = mg\dfrac{l}{4}$ and the gain in the kinetic energy of the rod will be $K = \dfrac{1}{2}I{\omega ^2}$, where $\omega $ is the angular velocity of the rod.
Then we have, $\dfrac{1}{2}I{\omega ^2} = mg\dfrac{l}{4}$ --------- (1).
Substituting for $I = \dfrac{{7m{l^2}}}{{48}}$ in equation (2) we get, $\dfrac{1}{2} \times \dfrac{{7m{l^2}}}{{48}}{\omega ^2} = mg\dfrac{l}{4}$
Cancelling similar terms on both sides of the above equation and simplifying it we get, $\dfrac{{7l}}{{48}}{\omega ^2} = \dfrac{g}{2}$
Then on rearranging, we have ${\omega ^2} = \dfrac{{48g}}{{14l}} = \dfrac{{24g}}{{7l}}$
Taking the square root on both sides of the above equation gives us $\omega = \sqrt {\dfrac{{24g}}{{7l}}} $
Thus the angular velocity of the rod is $\omega = \sqrt {\dfrac{{24g}}{{7l}}} $ .

Hence the correct option is C.

Note: Here, as the rod reaches the vertical position the force acting on it is the force of gravity. The centre of mass is at a height $\dfrac{l}{4}$ from the point of suspension. The gain in the rotational kinetic energy is, in fact, a change in the kinetic energy. The rod is initially in its horizontal position at rest. So the initial rotational kinetic energy is zero. This makes the gain in the kinetic energy equal to its final kinetic energy.