Question

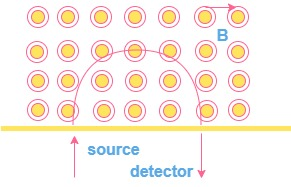
A uniform magnetic field with a slit system shown in fig. is to be used as a momentum filter for high energy charged particles. With a field B tesla, it is found that the filter transmits $ \alpha $ -particles each of energy $ 5\cdot 3 $ MeV. The magnetic field is increased to $ 2\cdot 3 $ B Tesla and deuterons are passed into the filter. The energy of each deuteron transmitted by the filter is…
(A) 5MeV
(B) 7MeV
(C) 14MeV
(D) 21MeV

Answer 1

Hint : The centripetal force required by the ion to move in a circular path is provided by the perpendicular magnetic field B.
 $ qvB=\dfrac{m{{v}^{2}}}{r} $
m is mass of charge particle to be accelerated, B is magnetic field, q is charge on particle, v is velocity of charge particle, r is radius of circular path.
The energy of particle is given $ E=\dfrac{{{p}^{2}}}{2m} $
p is the momentum of a particle.
Using the above formulas we will get the required result.


Complete step by step solution:
We have given, high energy charge particle in the magnetic field B Tesla.
Radius of charge particle is given by,
 $ \begin{align}
 & r=\dfrac{mv}{qB}=\dfrac{P}{qB} \\
 & \therefore r=\dfrac{\sqrt{2Em}}{Bq} \\
\end{align} $
Radius in case of $ \alpha $ -particles
    $ {{r}_{\alpha }}=\dfrac{{{\sqrt{2{{E}_{\alpha }}m}}_{\alpha }}}{B{{q}_{\alpha }}} $
Radius in case of deuteron –particle is given by
  $ {{r}_{d}}=\dfrac{{{\sqrt{2{{E}_{d}}m}}_{d}}}{2.3B{{q}_{d}}} $
Since the radius for both the particle is same
 $ \dfrac{{{\sqrt{2{{E}_{\alpha }}m}}_{\alpha }}}{B{{q}_{\alpha }}}=\dfrac{{{\sqrt{2{{E}_{d}}m}}_{d}}}{2\cdot 3B{{q}_{d}}} $
Squaring on both sides
   $ \dfrac{2{{E}_{\alpha }}{{m}_{\alpha }}}{{{q}_{\alpha }}^{2}}=\dfrac{2{{E}_{d}}{{m}_{d}}}{{{\left( 2\cdot 3 \right)}^{2}}{{q}_{d}}^{2}} $ ---- (1)
 Since,
   $ \dfrac{{{q}_{d}}}{{{q}_{\alpha }}}=\dfrac{e}{2e}=\dfrac{1}{2} $
qd is charge on deuteron, $ {{q}_{\alpha }} $ is charge on $ \alpha $ -particle
   $ \dfrac{{{m}_{\alpha }}}{{{m}_{d}}}=\dfrac{4}{2}=2 $
 $ {{m}_{\alpha }} $ is mass of $ \alpha $ -particle, $ {{m}_{d}} $ is mass of deuteron
 $ {{E}_{\alpha }} $ (energy of $ \alpha $ -particle = 5.3 MeV
Put all in eq. (1)
$ \begin{align}
& {{\left( 2.3 \right)}^{2}}\times {{\left( \dfrac{{{q}_{d}}}{{{q}_{\alpha }}} \right)}^{2}}\dfrac{{{E}_{\alpha }}{{m}_{\alpha }}}{{{m}_{d}}}={{E}_{d}} \\
& {{\left( 2.3 \right)}^{2}}\times {{\left( \dfrac{1}{2} \right)}^{2}}\times 5.3MeV(2)={{E}_{d}} \\
\end{align} $
Energy of deuteron particle is given by,
$ \begin{align}
& {{E}_{d}}={{\dfrac{\left( 2.3 \right)}{4}}^{2}}\times 2\times 5.3MeV \\
& {{E}_{d}}=14.01MeV \\
\end{align} $ .

Note:
Motion of charge particle in magnetic field explained below:
Then the centripetal force acquired by charged particle to move in circular path is provided by perpendicular magnetic field B is given by
$ {{F}_{e}}=\dfrac{m{{v}^{2}}}{r} $ --- (1)
$ {{F}_{b}}=qvB $ --- (2)
From eq (1) and (2)
$ \begin{align}
& \dfrac{m{{v}^{2}}}{r}=qvB \\
& \dfrac{mv}{r}=Bq \\
\end{align} $
$ r=\dfrac{mv}{qB} $ This is the radius of circular path.
The momentum of particle is given
$ P=mv $
And energy of particle is,
$ E=\dfrac{{{P}^{2}}}{2m} $
Or
$ P=\sqrt{2mE} $ ,
Radius of charge particle is given by
$ \begin{align}
& r=\dfrac{mv}{qB}=\dfrac{P}{qB} \\
& \therefore r=\dfrac{\sqrt{2Em}}{Bq} \\
\end{align} $.