
A taut string tension $100N$ and linear mass density $0.25kg/m$ is used inside a car to generate a wave pulse starting at the left end as shown. What should be the velocity of the cart so that the pulse remains stationary w.r.t. the ground?
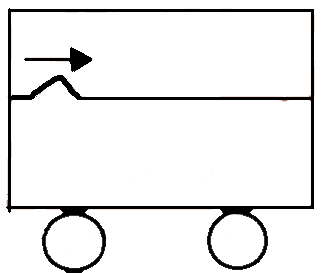
A) $-20i m/s$
B) $-30im/s$
C) $-40im/s$
D) $-50im/s$
Answer
233.1k+ views
Hint: In introduction to physics the pulses propagation on a taut string has always been an essential part. It illustrates uniform phase propagation, superposition and reflections which are concrete. It has more than obvious utility in string physics. Here, we need to find a relation between the tension in the string and the velocity. Put the given value and solve for the unknown.
Complete step by step solution:
The relationship between the tension and the velocity, it is given as:
\[S = \left( {\sqrt {\dfrac{T}{\mu }} } \right)\];
Here:
S = Velocity;
T = Tension;
\[\mu \]= Linear mass density;
Put the given value in the above equation:
\[S = \left( {\sqrt {\dfrac{T}{\mu }} } \right)\];
\[ \Rightarrow S = \left( {\sqrt {\dfrac{{100}}{{0.25}}} } \right)\];
Do, the necessary calculation:
\[ \Rightarrow S = \left( {\sqrt {\dfrac{{10000}}{{25}}} } \right)\];
\[ \Rightarrow S = \left( {\sqrt {400} } \right)\];
The value of the velocity is:
\[ \Rightarrow S = 20\]m/s;
$\overrightarrow {{V_P}} = \overrightarrow {{V_{PC}}} + \overrightarrow {{V_{CG}}} $;
Here:
$\overrightarrow {{V_P}} $= Velocity of pulse;
$\overrightarrow {{V_{PC}}} $= Velocity of pulse w.r.t. (relative) cart;
$\overrightarrow {{V_{CG}}} $= Velocity of cart w.r.t. (relative) ground;
$0 = 20 + \overrightarrow {{V_{CG}}} $;
$\overrightarrow {{V_{CG}}} = - 20i$;
Option (A) is correct. The velocity of the cart is -20i so that the pulse remains stationary w.r.t. the ground.
Note: Here the velocity of the cart should be opposite to the velocity of pulse w.r.t cart. Here, we need to see that the velocity of the cart is opposite as that is the only way to make the pulse look stationary while the pulse is moving in the positive direction.
Complete step by step solution:
The relationship between the tension and the velocity, it is given as:
\[S = \left( {\sqrt {\dfrac{T}{\mu }} } \right)\];
Here:
S = Velocity;
T = Tension;
\[\mu \]= Linear mass density;
Put the given value in the above equation:
\[S = \left( {\sqrt {\dfrac{T}{\mu }} } \right)\];
\[ \Rightarrow S = \left( {\sqrt {\dfrac{{100}}{{0.25}}} } \right)\];
Do, the necessary calculation:
\[ \Rightarrow S = \left( {\sqrt {\dfrac{{10000}}{{25}}} } \right)\];
\[ \Rightarrow S = \left( {\sqrt {400} } \right)\];
The value of the velocity is:
\[ \Rightarrow S = 20\]m/s;
$\overrightarrow {{V_P}} = \overrightarrow {{V_{PC}}} + \overrightarrow {{V_{CG}}} $;
Here:
$\overrightarrow {{V_P}} $= Velocity of pulse;
$\overrightarrow {{V_{PC}}} $= Velocity of pulse w.r.t. (relative) cart;
$\overrightarrow {{V_{CG}}} $= Velocity of cart w.r.t. (relative) ground;
$0 = 20 + \overrightarrow {{V_{CG}}} $;
$\overrightarrow {{V_{CG}}} = - 20i$;
Option (A) is correct. The velocity of the cart is -20i so that the pulse remains stationary w.r.t. the ground.
Note: Here the velocity of the cart should be opposite to the velocity of pulse w.r.t cart. Here, we need to see that the velocity of the cart is opposite as that is the only way to make the pulse look stationary while the pulse is moving in the positive direction.
Recently Updated Pages
Dimensions of Charge: Dimensional Formula, Derivation, SI Units & Examples

How to Calculate Moment of Inertia: Step-by-Step Guide & Formulas

Circuit Switching vs Packet Switching: Key Differences Explained

Dimensions of Pressure in Physics: Formula, Derivation & SI Unit

JEE General Topics in Chemistry Important Concepts and Tips

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




