Question

A tank is filled with water of density $1gc{m^{ - 3}}$ and oil of density $0.9gc{m^{ - 3}}$. The height of the water layer is 100cm and of the oil layer is 400cm. if $g = 980cm{s^{ - 2}}$, then the velocity of efflux from an opening in the bottom of the tank is:
A. $\sqrt {920 \times 980} cm{s^{ - 1}}$ ;
B. $\sqrt {900 \times 980} cm{s^{ - 1}}$;
C. $\sqrt {1000 \times 980} cm{s^{ - 1}}$;
D. $\sqrt {92 \times 980} cm{s^{ - 1}}$;

Answer 1

Hint:-We know the general formula for pressure which is $P = \dfrac{F}{A}$: P = pressure. F = force. A = area. And we know that mass is equal to density times volume. Write pressure in terms of density and form 2 equations for two tanks keeping the pressure the same, then write Torricelli’s equation and solve for the velocity of efflux.

Formula Used:
Here the formula used is:
$P = \dfrac{F}{A}$
Here:
P = pressure.
F = force.
A = area.
$m = d \times v$
m = mass.
d = density.
v = volume.
$v = \sqrt {2gh} $
v = velocity;
g = gravitational acceleration.
h = height.

Complete step-by-step solution:-
Step 1:
Formula for pressure:
$P = \dfrac{F}{A}$ ;
Here put F = ma.
$P = \dfrac{{ma}}{A}$;
Here $m = d \times v$;
$P = \dfrac{{d \times v \times a}}{A}$;
Write the units of area and volume
$P = \dfrac{{\rho \times {m^3} \times a}}{{{m^2}}}$;
Here d = density =$\rho $.
$P = \rho \times m \times a$;
Here m = meter = height = h;
$P = \rho \times h \times a$

Step 2: Here, the pressure that is put on the opening in the water (See the diagram on LHS) tank is equal to the pressure that is put on the water tank with height h (See the diagram on RHS).

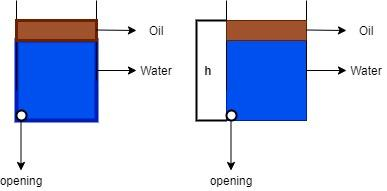
\[h{\rho _w}g = {h_o}{\rho _o}g + {h_w}{\rho _w}g\]; …(a = g)
\[h{\rho _w}g = 4 \times 0.9 \times 9.8 + 1 \times 1 \times 9.8\];
\[h \times 10 = 4 \times 0.9 \times 9.8 + 1 \times 1 \times 9.8\]
\[h = 4.6m\];

Step 3:
Apply Torricelli's equation.
$v = \sqrt {2gh} $ ;
Put the given values. Here $g = 9.8m/{s^2}$
$v = \sqrt {2 \times 9.8 \times 4.6} $
$v = \sqrt {9.8 \times 9.2} {\text{ }}m/s$;
Now convert it into cm/s.
$v = \sqrt {920 \times 980{\text{ }}} {\text{c}}m/s$
Final Answer: Option “1” is correct.

Note:- Here first write the general formula for pressure, then write it in terms of density and equate it with a similar equation for another tank where the weight of oil and water are combined. After getting the height apply the Torricelli’s equation and find out the velocity.