A tangent to the parabola ${{x}^{2}}+4ay=0$ cuts the parabola ${{x}^{2}}=4by$, at A and B the locus of the midpoint of AB is
(a) $\left( a+2b \right){{x}^{2}}=4{{b}^{2}}y$
(b) $\left( b+2a \right){{x}^{2}}=4{{b}^{2}}y$
(c) $\left( a+2b \right){{y}^{2}}=4{{b}^{2}}x$
(d) $\left( b+2a \right){{x}^{2}}=4{{a}^{2}}y$
Answer
Verified361.8k+ views
Hint: Write equation of tangent on the parabola ${{x}^{2}}+4ay=0$. And find the intersection of tangent and the parabola ${{x}^{2}}=4by$. Don’t calculate the exact coordinates. Try to use the equation to get locus of the mid-points of A and B.
Complete step-by-step answer:
Let us suppose a parametric coordinate on parabola ${{x}^{2}}+4ay=0$ as $\left( 2at,-a{{t}^{2}} \right)$.
Now, we can write the equation of tangent through this point by T=0.
If $\left( {{x}_{1,}}{{y}_{1}} \right)$is a point on parabola, ${{x}^{2}}=-4ay$, then tangent through it is given as
$x{{x}_{1}}=-4a\dfrac{\left( y+{{y}_{1}} \right)}{2}=-2a\left( y+{{y}_{1}} \right)$
As, we have points $\left( {{x}_{1,}}{{y}_{1}} \right)$ as $\left( 2at,-a{{t}^{2}} \right)$.
Hence tangent through it be
$\begin{align}
& x\left( 2at \right)=-2a\left( y+\left( -a{{t}^{2}} \right) \right) \\
& \Rightarrow 2atx=-2a\left( y-a{{t}^{2}} \right) \\
& \Rightarrow atx+ay-{{a}^{2}}{{t}^{2}}=0 \\
& \Rightarrow tx+y-a{{t}^{2}}=0............(i) \\
\end{align}$
Now, let us suppose, tangent is intersecting the parabola ${{x}^{2}}=4by$ at points $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{x}},{{y}_{2}} \right)$ and mid-point of them as (h,k).
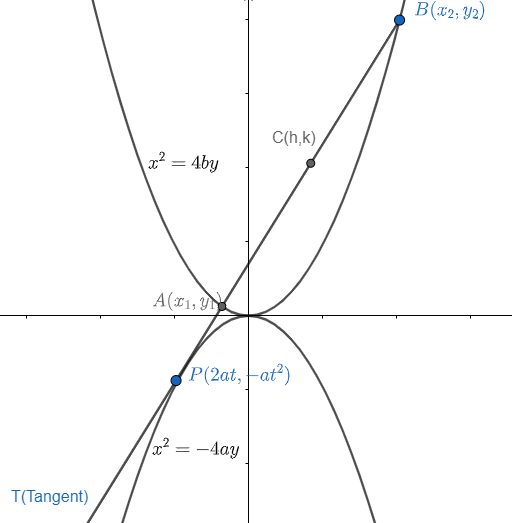
Let us find the intersection points of parabola ${{x}^{2}}=4by$ and the tangent ‘T’ on ${{x}^{2}}=-4ay$.
So, from equation ${{x}^{2}}=4by$, we get
$y=\dfrac{{{x}^{2}}}{4b}$ ………………….. (ii)
Putting value of ‘y’ from equation (ii) in equation (i), we get
$\begin{align}
& tx+\dfrac{{{x}^{2}}}{4b}-a{{t}^{2}}=0 \\
& \Rightarrow {{x}^{2}}+4btx-4ab{{t}^{2}}=0..........(iii) \\
\end{align}$
As above equation is a quadratic equation so, we can get values of $\left( {{x}_{1}},{{x}_{2}} \right)$ as roots of equation (iii).
Now, we know the relation of roots with the coefficients of quadratic equation which is given as
$\text{sum of roots = - }\dfrac{\text{coefficient of x}}{\text{coefficient of }{{\text{x}}^{\text{2}}}}$ ……….. (iv)
$\text{product of roots = }\dfrac{\text{constant term}}{\text{coefficient of }{{\text{x}}^{\text{2}}}}$ ……………. (v)
Now, from equation (iii), (iv) and (v), we get
${{x}_{1}}+{{x}_{2}}=-4bt$ ………………. (vi)
${{x}_{2}}+{{x}_{2}}=4ab{{t}^{2}}$ ……………… (vii)
Similarly, we can get a quadratic in ‘y’ if we put value of ‘x’ from equation of tangent i.e. $tx+y-a{{t}^{2}}=0$ in equation of parabola ${{x}^{2}}=4by$. Hence, we get
${{\left( \dfrac{a{{t}^{2}}-y}{t} \right)}^{2}}=4by$
Now, use ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ , we get
$\begin{align}
& \dfrac{{{a}^{2}}{{t}^{4}}+{{y}^{2}}-2ay{{t}^{2}}}{{{t}^{2}}}=4by \\
& \Rightarrow {{y}^{2}}-2a{{t}^{2}}y-4b{{t}^{2}}y+{{a}^{2}}{{t}^{4}}=0 \\
& \Rightarrow {{y}^{2}}-\left( 2a{{t}^{2}}+4b{{t}^{2}} \right)y+{{a}^{2}}+{{t}^{4}}=0.......(viii) \\
\end{align}$
Now, ${{y}_{1}}$ and ${{y}_{2}}$ are roots of above equation hence from equation (iv) and (v), we get
${{y}_{1}}+{{y}_{2}}=2a{{t}^{2}}+4b{{t}^{2}}$ …………….. (ix)
${{y}_{1}}{{y}_{2}}={{a}^{2}}{{t}^{4}}$……………. (x)
Now, as we need to find locus of midpoint of AB which can be given as
$h=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and $k=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$
Hence, from equation (vi) and (ix), we get
$h=\dfrac{-4bt}{2}$ and $k=\dfrac{2a{{t}^{2}}+4b{{t}^{2}}}{2}$
H=-2bt and $k=\dfrac{2a{{t}^{2}}}{2}+\dfrac{4b{{t}^{2}}}{2}=a{{t}^{2}}+2b{{t}^{2}}$
Now, we can eliminate ‘t’ by substituting value of ‘t’ from relation h and t to relation ‘k’ and ’t’, hence, we get so, we have
$t=\dfrac{-h}{2b}$
And hence
$\begin{align}
& k=a{{\left( \dfrac{-h}{2b} \right)}^{2}}+2b{{\left( \dfrac{-h}{2b} \right)}^{2}} \\
& k=\dfrac{{{h}^{2}}a}{4{{b}^{2}}}+\dfrac{2b{{h}^{2}}}{4{{b}^{2}}} \\
\end{align}$
Now, replacing (h, k) by (x, y) to get the required locus. Hence, we get
$\begin{align}
& y=\dfrac{{{x}^{2}}a}{4{{b}^{2}}}+\dfrac{2b{{x}^{2}}}{4{{b}^{2}}} \\
& 4{{b}^{2}}y={{x}^{2}}\left( a+2b \right) \\
\end{align}$
Hence, option (a) is the correct answer.
Note: Another approach for the given problem would be that we can suppose parametric coordinates of points A and B lying on ${{x}^{2}}=4by$. And write the equation of line passing through A and B. Now, this line is acting as a tangent for ${{x}^{2}}=-4ay$. So, intersection of them would be the only point. So, use this condition to get equations in parametric variables and hence get locus of midpoint of A and B.
One can suppose parametric coordinates at ${{x}^{2}}=-4ay$ as $\left( -2at,-a{{t}^{2}} \right)$as well.
Calculation is the important side of the problem as well. So, take care of it.
Writing tangent equation through point $\left( {{x}_{1}},{{y}_{1}} \right)$ on any curve f(x)=0 is given by replacing
$\begin{align}
& {{\text{x}}^{\text{2}}}\text{ by x}{{\text{x}}_{\text{1}}} \\
& {{\text{y}}^{\text{2}}}\text{ by y}{{\text{y}}_{\text{1}}} \\
& \text{x by }\dfrac{\text{x+}{{\text{x}}_{\text{1}}}}{\text{2}} \\
& \text{y by }\dfrac{\text{y+}{{\text{y}}_{\text{1}}}}{\text{2}} \\
\end{align}$
Complete step-by-step answer:
Let us suppose a parametric coordinate on parabola ${{x}^{2}}+4ay=0$ as $\left( 2at,-a{{t}^{2}} \right)$.
Now, we can write the equation of tangent through this point by T=0.
If $\left( {{x}_{1,}}{{y}_{1}} \right)$is a point on parabola, ${{x}^{2}}=-4ay$, then tangent through it is given as
$x{{x}_{1}}=-4a\dfrac{\left( y+{{y}_{1}} \right)}{2}=-2a\left( y+{{y}_{1}} \right)$
As, we have points $\left( {{x}_{1,}}{{y}_{1}} \right)$ as $\left( 2at,-a{{t}^{2}} \right)$.
Hence tangent through it be
$\begin{align}
& x\left( 2at \right)=-2a\left( y+\left( -a{{t}^{2}} \right) \right) \\
& \Rightarrow 2atx=-2a\left( y-a{{t}^{2}} \right) \\
& \Rightarrow atx+ay-{{a}^{2}}{{t}^{2}}=0 \\
& \Rightarrow tx+y-a{{t}^{2}}=0............(i) \\
\end{align}$
Now, let us suppose, tangent is intersecting the parabola ${{x}^{2}}=4by$ at points $A\left( {{x}_{1}},{{y}_{1}} \right)$ and $B\left( {{x}_{x}},{{y}_{2}} \right)$ and mid-point of them as (h,k).
Let us find the intersection points of parabola ${{x}^{2}}=4by$ and the tangent ‘T’ on ${{x}^{2}}=-4ay$.
So, from equation ${{x}^{2}}=4by$, we get
$y=\dfrac{{{x}^{2}}}{4b}$ ………………….. (ii)
Putting value of ‘y’ from equation (ii) in equation (i), we get
$\begin{align}
& tx+\dfrac{{{x}^{2}}}{4b}-a{{t}^{2}}=0 \\
& \Rightarrow {{x}^{2}}+4btx-4ab{{t}^{2}}=0..........(iii) \\
\end{align}$
As above equation is a quadratic equation so, we can get values of $\left( {{x}_{1}},{{x}_{2}} \right)$ as roots of equation (iii).
Now, we know the relation of roots with the coefficients of quadratic equation which is given as
$\text{sum of roots = - }\dfrac{\text{coefficient of x}}{\text{coefficient of }{{\text{x}}^{\text{2}}}}$ ……….. (iv)
$\text{product of roots = }\dfrac{\text{constant term}}{\text{coefficient of }{{\text{x}}^{\text{2}}}}$ ……………. (v)
Now, from equation (iii), (iv) and (v), we get
${{x}_{1}}+{{x}_{2}}=-4bt$ ………………. (vi)
${{x}_{2}}+{{x}_{2}}=4ab{{t}^{2}}$ ……………… (vii)
Similarly, we can get a quadratic in ‘y’ if we put value of ‘x’ from equation of tangent i.e. $tx+y-a{{t}^{2}}=0$ in equation of parabola ${{x}^{2}}=4by$. Hence, we get
${{\left( \dfrac{a{{t}^{2}}-y}{t} \right)}^{2}}=4by$
Now, use ${{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ , we get
$\begin{align}
& \dfrac{{{a}^{2}}{{t}^{4}}+{{y}^{2}}-2ay{{t}^{2}}}{{{t}^{2}}}=4by \\
& \Rightarrow {{y}^{2}}-2a{{t}^{2}}y-4b{{t}^{2}}y+{{a}^{2}}{{t}^{4}}=0 \\
& \Rightarrow {{y}^{2}}-\left( 2a{{t}^{2}}+4b{{t}^{2}} \right)y+{{a}^{2}}+{{t}^{4}}=0.......(viii) \\
\end{align}$
Now, ${{y}_{1}}$ and ${{y}_{2}}$ are roots of above equation hence from equation (iv) and (v), we get
${{y}_{1}}+{{y}_{2}}=2a{{t}^{2}}+4b{{t}^{2}}$ …………….. (ix)
${{y}_{1}}{{y}_{2}}={{a}^{2}}{{t}^{4}}$……………. (x)
Now, as we need to find locus of midpoint of AB which can be given as
$h=\dfrac{{{x}_{1}}+{{x}_{2}}}{2}$ and $k=\dfrac{{{y}_{1}}+{{y}_{2}}}{2}$
Hence, from equation (vi) and (ix), we get
$h=\dfrac{-4bt}{2}$ and $k=\dfrac{2a{{t}^{2}}+4b{{t}^{2}}}{2}$
H=-2bt and $k=\dfrac{2a{{t}^{2}}}{2}+\dfrac{4b{{t}^{2}}}{2}=a{{t}^{2}}+2b{{t}^{2}}$
Now, we can eliminate ‘t’ by substituting value of ‘t’ from relation h and t to relation ‘k’ and ’t’, hence, we get so, we have
$t=\dfrac{-h}{2b}$
And hence
$\begin{align}
& k=a{{\left( \dfrac{-h}{2b} \right)}^{2}}+2b{{\left( \dfrac{-h}{2b} \right)}^{2}} \\
& k=\dfrac{{{h}^{2}}a}{4{{b}^{2}}}+\dfrac{2b{{h}^{2}}}{4{{b}^{2}}} \\
\end{align}$
Now, replacing (h, k) by (x, y) to get the required locus. Hence, we get
$\begin{align}
& y=\dfrac{{{x}^{2}}a}{4{{b}^{2}}}+\dfrac{2b{{x}^{2}}}{4{{b}^{2}}} \\
& 4{{b}^{2}}y={{x}^{2}}\left( a+2b \right) \\
\end{align}$
Hence, option (a) is the correct answer.
Note: Another approach for the given problem would be that we can suppose parametric coordinates of points A and B lying on ${{x}^{2}}=4by$. And write the equation of line passing through A and B. Now, this line is acting as a tangent for ${{x}^{2}}=-4ay$. So, intersection of them would be the only point. So, use this condition to get equations in parametric variables and hence get locus of midpoint of A and B.
One can suppose parametric coordinates at ${{x}^{2}}=-4ay$ as $\left( -2at,-a{{t}^{2}} \right)$as well.
Calculation is the important side of the problem as well. So, take care of it.
Writing tangent equation through point $\left( {{x}_{1}},{{y}_{1}} \right)$ on any curve f(x)=0 is given by replacing
$\begin{align}
& {{\text{x}}^{\text{2}}}\text{ by x}{{\text{x}}_{\text{1}}} \\
& {{\text{y}}^{\text{2}}}\text{ by y}{{\text{y}}_{\text{1}}} \\
& \text{x by }\dfrac{\text{x+}{{\text{x}}_{\text{1}}}}{\text{2}} \\
& \text{y by }\dfrac{\text{y+}{{\text{y}}_{\text{1}}}}{\text{2}} \\
\end{align}$
Last updated date: 27th Sep 2023
•
Total views: 361.8k
•
Views today: 8.61k
Recently Updated Pages
Trending doubts
How do you solve x2 11x + 28 0 using the quadratic class 10 maths CBSE
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE
Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE
Difference Between Plant Cell and Animal Cell
One cusec is equal to how many liters class 8 maths CBSE
The equation xxx + 2 is satisfied when x is equal to class 10 maths CBSE
What is the color of ferrous sulphate crystals? How does this color change after heating? Name the products formed on strongly heating ferrous sulphate crystals. What type of chemical reaction occurs in this type of change.
Give 10 examples for herbs , shrubs , climbers , creepers
Change the following sentences into negative and interrogative class 10 english CBSE