Question

A swimmer S is in the sea at a distance ’d’ km from the closest point A on a straight shore. The house of the swimmer is one the shore at a distance \[L{\text{ km}}\] from A. He can swim at a speed of \[u{\text{ km/hr}}\] and walk at a speed of \[v{\text{ km/hr}}\left( {v > u} \right)\]. At which point on the shore should he land so that he reaches his house in the shortest possible time?
A. \[\dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}\]
B. \[\dfrac{{vd}}{{\sqrt {{v^2} - {u^2}} }}\]
C. \[\dfrac{{vd}}{{\sqrt {{v^2} + {u^2}} }}\]
D. \[\dfrac{{ud}}{{\sqrt {{v^2} + {u^2}} }}\]

Answer 1

Hint: First of all, draw the figure for this problem with the help of the given data to get a clear idea of what we have to find. Then use the distance-time formula and second derivative test to find the shortest time period. So, use this concept to reach the solution to the given problem.

Complete step-by-step solution:
Given that the swimmer is at a point S which is at a distance ‘d’ km from point A.
Let the house of the swimmer be at point B.
Since the distance between point A and his house i.e., B is \[L{\text{ km}}\]. So, \[AB = L{\text{ km}}\].
Let the swimmer land at point C on the shore and let \[AC = x{\text{ km}}\]as shown in the below figure:

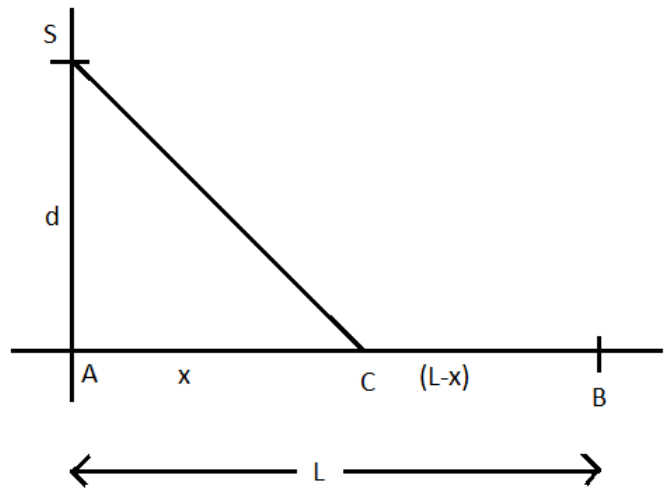
Therefore, from the figure \[SC = \sqrt {{x^2} + {d^2}} \] and \[CB = \left( {L - x} \right)\]
We know that \[{\text{time}} = \dfrac{{{\text{distance}}}}{{{\text{speed}}}}\]
Given that speed of the swimmer to swim from S to C \[ = u{\text{ km/hr}}\]
So, time taken to travel from S to C \[ = \dfrac{{\sqrt {{x^2} + {d^2}} }}{u}\]
Also given that speed of the swimmer to walk from C to B \[ = v{\text{ km/hr}}\]
So, time taken to travel from S to B \[ = \dfrac{{L - x}}{v}\]
Let \[T\] be the time taken to travel from S to B
time taken to travel from S to B = time taken to travel from S to C + time taken to travel from C to B
\[ \Rightarrow T = \dfrac{{\sqrt {{x^2} + {d^2}} }}{u} + \dfrac{{L - x}}{v}\]
Let \[f\left( x \right) = T = \dfrac{{\sqrt {{x^2} + {d^2}} }}{u} + \dfrac{L}{v} - \dfrac{x}{v}\]
Differentiating \[f\left( x \right)\] with respective to \[x\], we have
\[
   \Rightarrow f'\left( x \right) = \dfrac{d}{{dx}}\left( {\dfrac{{\sqrt {{x^2} + {d^2}} }}{u}} \right) + \dfrac{d}{{dx}}\left( {\dfrac{L}{v}} \right) - \dfrac{d}{{dx}}\left( {\dfrac{x}{v}} \right) \\
   \Rightarrow f'\left( x \right) = \dfrac{1}{u}\dfrac{d}{{dx}}\left( {\sqrt {{x^2} + {d^2}} } \right) + \dfrac{d}{{dx}}\left( {\dfrac{L}{v}} \right) - \dfrac{1}{v}\dfrac{d}{{dx}}\left( x \right) \\
   \Rightarrow f'\left( x \right) = \dfrac{1}{u}.\dfrac{{2x}}{{2\sqrt {{x^2} + {d^2}} }} + 0 - \dfrac{1}{v} \\
\]
We know that for the least and greatest value of any function is obtained by equating its first derivate to zero.
For maximum or minimum, put \[f'\left( x \right) = 0\]
\[
   \Rightarrow \dfrac{1}{u}.\dfrac{{2x}}{{2\sqrt {{x^2} + {d^2}} }} + 0 - \dfrac{1}{v} = 0 \\
   \Rightarrow \dfrac{x}{{u\sqrt {{x^2} + {d^2}} }} = \dfrac{1}{v} \\
   \Rightarrow \dfrac{{\sqrt {{x^2} + {d^2}} }}{x} = \dfrac{v}{u} \\
\]
Squaring on both sides, we get
\[
   \Rightarrow \dfrac{{{x^2} + {d^2}}}{{{x^2}}} = \dfrac{{{v^2}}}{{{u^2}}} \\
   \Rightarrow \dfrac{{{x^2}}}{{{x^2}}} + \dfrac{{{d^2}}}{{{x^2}}} = \dfrac{{{v^2}}}{{{u^2}}} \\
   \Rightarrow 1 + \dfrac{{{d^2}}}{{{x^2}}} = \dfrac{{{v^2}}}{{{u^2}}} \\
   \Rightarrow \dfrac{{{d^2}}}{{{x^2}}} = \dfrac{{{v^2}}}{{{u^2}}} - 1 \\
   \Rightarrow \dfrac{{{d^2}}}{{{x^2}}} = \dfrac{{{v^2} - {u^2}}}{{{u^2}}} \\
   \Rightarrow {x^2} = \dfrac{{{u^2}{d^2}}}{{{v^2} - {u^2}}} \\
\]
Rooting on both sides, we have
\[
   \Rightarrow x = \pm \dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }} \\
  \therefore x = \dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}{\text{ or }}\dfrac{{ - ud}}{{\sqrt {{v^2} - {u^2}} }} \\
\]
We know that, the least value is obtained for the value of \[x\] at which \[\dfrac{{{d^2}f\left( x \right)}}{{d{x^2}}} > 0\] and the greatest value is obtained for the value of \[x\] at which \[\dfrac{{{d^2}f\left( x \right)}}{{d{x^2}}} < 0\].
Now, consider the second derivative of \[f\left( x \right)\]
\[ \Rightarrow f''\left( x \right) = \dfrac{d}{{dx}}\left( {f'\left( x \right)} \right) = \dfrac{d}{{dx}}\left( {\dfrac{x}{{u\sqrt {{x^2} + {d^2}} }}} \right)\]
\[
   \Rightarrow f''\left( x \right) = \dfrac{d}{{dx}}\left( {f'\left( x \right)} \right) = \dfrac{d}{{dx}}\left( {\dfrac{x}{{u\sqrt {{x^2} + {d^2}} }}} \right) \\
  \therefore f''\left( x \right) = \dfrac{{{d^2}}}{{u\left( {{x^2} + {d^2}} \right)\sqrt {{x^2} + {d^2}} }} \\
\]
For \[x = \dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}\] we have \[f''\left( {\dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}} \right) > 0\].
So, the shortest possible time is \[\dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}\].
Thus, the correct option is A. \[\dfrac{{ud}}{{\sqrt {{v^2} - {u^2}} }}\]

Note: For the least and greatest value of any function is obtained by equating its first derivate to zero. The least value is obtained for the value of \[x\] at which \[\dfrac{{{d^2}f\left( x \right)}}{{d{x^2}}} > 0\] and the greatest value is obtained for the value of \[x\] at which \[\dfrac{{{d^2}f\left( x \right)}}{{d{x^2}}} < 0\].