Question

A series RLC circuit has a bandwidth of 300rad/sec at a resonance frequency of 3000rad/sec when excited by a voltage source of 100V. The inductance of the coil is 0.1H. The value of R and voltage across C are respectively
$\begin{align}
  & \left( 1 \right)10\Omega and 100V \\
 & \left( 2 \right)30\Omega and 100V \\
 & \left( 3 \right)30\Omega and 1000V \\
 & \left( 4 \right)300\Omega and 1000V \\
\end{align}$

Answer 1

Hint: Here the bandwidth is the ratio of the given resistance and the inductance in the circuit. Hence by rearranging the equation we get the equation of R. Then by substituting the values of the bandwidth and the inductance we will the resistance. The quality factor is the ratio of resonant frequency to the band width. The product of the quality factor and source voltage is equal to the voltage across capacitance which is also equal to the voltage across inductance.

Complete answer:

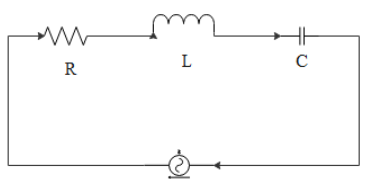
Given that V=100V
L=0.1H
Band width =300rad/sec
In series RLC circuit,
$Bandwidth=\dfrac{R}{L}=300$
$\Rightarrow $ $R=Bandwidth\times L$
$\Rightarrow R=300\times 0.1$
$\therefore R=30\Omega $
$Q=\dfrac{\operatorname{Re}sonantFrequency}{bandwidth}$
where, Q is the quality factor.
$\begin{align}
  & \Rightarrow Q=\dfrac{3000}{300} \\
 & \therefore Q=10 \\
\end{align}$
At resonance,
$\left| {{V}_{L}} \right|=\left| {{V}_{C}} \right|=Q{{V}_{S}}$
$\begin{align}
  & \Rightarrow Q{{V}_{S}}=10\times 100 \\
 & \therefore \left| {{V}_{L}} \right|=\left| {{V}_{C}} \right|=1000V \\
\end{align}$

Hence option (3) is correct.

Additional information:
Inductive reactance is the name given to a changing current flow. The impedance is usually measured in ohms, just like resistance. That is, the inductive reactance has the same unit of resistance. Capacitive reactance decreases with the increasing value of AC frequency, while inductive reactance increases with increasing AC frequency. When current passes through a coil, then it will become electromagnetic. The current that flows through the coil will have an opposition like resistance upon its inductance and frequency waveform. Where inductive reactance is the product of inductance and angular frequency. Similarly, capacitive reactance is the product of capacitance and angular frequency. By substituting these values and substituting we get the value of capacitance.

Note:
The quality factor is the ratio of resonant frequency to the band width. The product of the quality factor and source voltage is equal to the voltage across capacitance which is also equal to the voltage across inductance. Also the bandwidth is the ratio of the given resistance and the inductance in the circuit.