Question

A person 1.6m tall is standing at the centre between two walls three meter high. What is the minimum size of plane mirror fixed on the wall in front of him, if he is to see the full height of the wall behind him?

Answer 1

Hint: We are able to see that object from which light falls on our eyes, either directly or indirectly. The light may be reflected or self-produced (in case of luminous objects). In case we want to view a full object having some dimensions, the light from the left and right most corners and from the bottom and top most corner must fall on the eyes.

Complete answer:

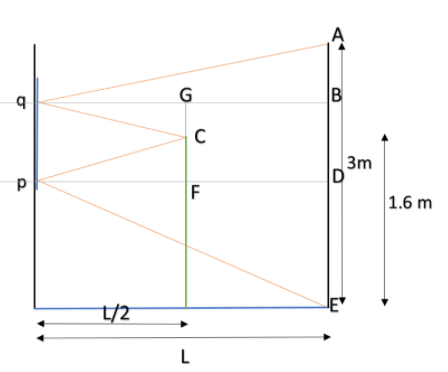
From this detailed figure, we can see that for minimum width of mirror, the rays from the head of the boy (C), has to strike the extremities of mirror ‘pq’.
Now, from similar triangles, we have;
$\dfrac{AB}{GC} = \dfrac{qB}{qG} = \dfrac{L}{L/2} = 2$
Thus AB = 2GC
Similarly, DE = 2CF
To find;
$qp = GC + CF = \dfrac{AB}{2} + \dfrac{DE}{2}$
$\implies AB + DE = 2qp$
Also $AB + BD + DE = 3$
$BD + AB + DE = BD + 2qp = 3$
Now $GF = BD = pq$
Thus, $pq+2pq = 3$
$\implies pq = 1 m$
Hence, the minimum width of the mirror should be 1 m.

Additional information:
We can see that we didn’t use the height of a person. So, to calculate the minimum width of the mirror required to view the full wall, we don’t need a person. But for a shorter person, the position of the mirror and the position at which the person is standing do matter.

Note:
These type of questions can be easily solved by using the symmetry rather than equations. The person just needs the upper point of the wall and the lower end of the wall. One can neglect the effect of two eyes present as the distance between two eyes is very small as compared to the 3m wall. One can get confused why the triangles are similar here. This is because the rays follow laws of reflection. Thus angle of incidence is equal to the angle of reflection.