
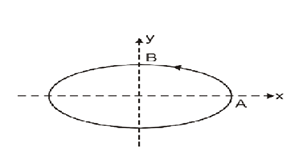
A particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration is:
A) Continuously increases.
B) Continuously decreases.
C) Remains constant.
D) First increases and then decreases.
Answer
233.1k+ views
Hint: As we know that If the particle is moving with a constant velocity or speed in an elliptical path, then the motion is said to be accelerated motion, so the direction of the velocity changes at every point of elliptical path.
Complete step by step answer:
Consider the question, we are given that a particle is moving along an elliptical path with a constant speed. And the particle moves from point \[A\] to point \[B\].
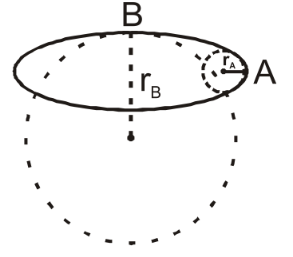
To understand the given information, when the particle is moving from \[A\] to point \[B\], we can observe from the figure\[\left( 2 \right)\] that radius is increasing continuously.
We are given the constant speed, so, the speed on the tangent will be zero.
\[ \Rightarrow {a_t} = \dfrac{{dv}}{{dt}}\]
Therefore, the tangential acceleration will be zero.
\[ \Rightarrow {a_t} = 0\]
Now we will consider the radius of the curvature of the circle \[R\], and the acceleration of the curvature is \[{a_c}\] when the particle is moving towards the \[B\] point.
\[ \Rightarrow {a_c} = \dfrac{{{v^2}}}{R}\]
As the speed of the particle is constant, when the particle moves from A to B, the magnitude of its acceleration is decreasing because the radius of the curvature is increasing.
Therefore, when the particle is moving from A to B then the magnitude of its acceleration is continuously decreasing.
So, the option (B) is correct.
Note: In this question, as we know that the acceleration is the rate of change of the velocity. Here, the particle moves from point \[A\] to point \[B\], then the velocity or speed of the particle is constant. So, the acceleration of the particle will be zero.
Complete step by step answer:
Consider the question, we are given that a particle is moving along an elliptical path with a constant speed. And the particle moves from point \[A\] to point \[B\].
To understand the given information, when the particle is moving from \[A\] to point \[B\], we can observe from the figure\[\left( 2 \right)\] that radius is increasing continuously.

We are given the constant speed, so, the speed on the tangent will be zero.
\[ \Rightarrow {a_t} = \dfrac{{dv}}{{dt}}\]
Therefore, the tangential acceleration will be zero.
\[ \Rightarrow {a_t} = 0\]
Now we will consider the radius of the curvature of the circle \[R\], and the acceleration of the curvature is \[{a_c}\] when the particle is moving towards the \[B\] point.
\[ \Rightarrow {a_c} = \dfrac{{{v^2}}}{R}\]
As the speed of the particle is constant, when the particle moves from A to B, the magnitude of its acceleration is decreasing because the radius of the curvature is increasing.
Therefore, when the particle is moving from A to B then the magnitude of its acceleration is continuously decreasing.
So, the option (B) is correct.
Note: In this question, as we know that the acceleration is the rate of change of the velocity. Here, the particle moves from point \[A\] to point \[B\], then the velocity or speed of the particle is constant. So, the acceleration of the particle will be zero.
Recently Updated Pages
JEE Main 2026 Session 2 Registration Open, Exam Dates, Syllabus & Eligibility

JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

Trending doubts
JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding Average and RMS Value in Electrical Circuits

Understanding Collisions: Types and Examples for Students

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Understanding Atomic Structure for Beginners

Derive an expression for maximum speed of a car on class 11 physics JEE_Main

Other Pages
JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry

NCERT Solutions For Class 11 Physics Chapter 9 Mechanical Properties of Fluids (2025-26)

NCERT Solutions For Class 11 Physics Chapter 12 Kinetic Theory (2025-26)

NCERT Solutions For Class 11 Physics Chapter 4 Law of Motion (2025-26)

Class 11 JEE Main Physics Mock Test 2025

Inductive Effect and Its Role in Acidic Strength




