
Derive an expression for maximum speed of a car on a banked road in circular motion.
Answer
538.4k+ views
Hint:In this question, we need to find the maximum speed of the car at which car doesn’t skid while moving in a circular banked road. We basically balance all the factors of the forces exerted on a car in x-axis direction and y-axis direction.
To solve any balancing problems, whether motion is translational or rotational, we always balance forces acting along x-axis and y-axis.
In case of rotational motion, we balance torques acting on the body.
Complete step-by-step answer:
Several formulas used in our calculations are-
Gravitational attraction force – mg
Frictional force (f) – acting between car’s tire and road, and parallel to the slope of road
Normal force (N)- It is a reaction force of the gravitational force exerted by the road on car
Centripetal force $\left( \dfrac{m{{v}^{2}}}{r} \right)$ - acting towards the center of the circular path followed by the car.
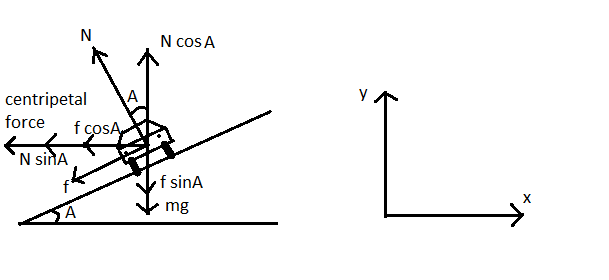
Let’s take inclination angle A of road with respect to the x-axis as shown in the above diagram. Now we can balance all the x-axis and y-axis factors of forces. Refer to the figure.
(1) Balancing all the forces acting along the x-axis-
$f\cos (A)+N\sin (A)=\dfrac{m{{v}^{2}}}{r}$
Substituting the value $f=\mu N$ into equation, we get
$\begin{align}
& \mu N\cos (A)+N\sin (A)=\dfrac{m{{v}^{2}}}{r} \\
& \Rightarrow N\left( \mu \cos A+\sin A \right)=\dfrac{m{{v}^{2}}}{r}......(1) \\
\end{align}$
(2) Balancing all the forces acting along the y-axis-
$\begin{align}
& N\cos A=f\sin A+mg \\
& \Rightarrow N\cos A=\mu N\sin A+mg \\
& \Rightarrow N\left( \cos A-\mu \sin A \right)=mg........(2) \\
\end{align}$
(3) Frictional force-
$f=\mu N$
Now we will use these three equations to find the value of speed (v).
Now we can divide equation (1) and (2), we get
\[\begin{align}
& \dfrac{{{v}^{2}}}{rg}=\dfrac{\left( \mu +\tan A \right)}{\left( 1-\mu \tan A \right)} \\
& \Rightarrow v=\sqrt{\dfrac{rg\left( \mu +\tan A \right)}{\left( 1-\mu \tan A \right)}} \\
\end{align}\]
This is an expression for maximum speed of a car on a banked road in circular motion.
Note: (1) Roads are banked to prevent high speed cars from skidding.
(2) If a car is moving at a speed more than mentioned above, it will skid.
(3) If the force of friction is not strong enough, the vehicle will skid. Also, note that friction acts downwards along the road, as the tendency of the car is to skid up.
To solve any balancing problems, whether motion is translational or rotational, we always balance forces acting along x-axis and y-axis.
In case of rotational motion, we balance torques acting on the body.
Complete step-by-step answer:
Several formulas used in our calculations are-
Gravitational attraction force – mg
Frictional force (f) – acting between car’s tire and road, and parallel to the slope of road
Normal force (N)- It is a reaction force of the gravitational force exerted by the road on car
Centripetal force $\left( \dfrac{m{{v}^{2}}}{r} \right)$ - acting towards the center of the circular path followed by the car.

Let’s take inclination angle A of road with respect to the x-axis as shown in the above diagram. Now we can balance all the x-axis and y-axis factors of forces. Refer to the figure.
(1) Balancing all the forces acting along the x-axis-
$f\cos (A)+N\sin (A)=\dfrac{m{{v}^{2}}}{r}$
Substituting the value $f=\mu N$ into equation, we get
$\begin{align}
& \mu N\cos (A)+N\sin (A)=\dfrac{m{{v}^{2}}}{r} \\
& \Rightarrow N\left( \mu \cos A+\sin A \right)=\dfrac{m{{v}^{2}}}{r}......(1) \\
\end{align}$
(2) Balancing all the forces acting along the y-axis-
$\begin{align}
& N\cos A=f\sin A+mg \\
& \Rightarrow N\cos A=\mu N\sin A+mg \\
& \Rightarrow N\left( \cos A-\mu \sin A \right)=mg........(2) \\
\end{align}$
(3) Frictional force-
$f=\mu N$
Now we will use these three equations to find the value of speed (v).
Now we can divide equation (1) and (2), we get
\[\begin{align}
& \dfrac{{{v}^{2}}}{rg}=\dfrac{\left( \mu +\tan A \right)}{\left( 1-\mu \tan A \right)} \\
& \Rightarrow v=\sqrt{\dfrac{rg\left( \mu +\tan A \right)}{\left( 1-\mu \tan A \right)}} \\
\end{align}\]
This is an expression for maximum speed of a car on a banked road in circular motion.
Note: (1) Roads are banked to prevent high speed cars from skidding.
(2) If a car is moving at a speed more than mentioned above, it will skid.
(3) If the force of friction is not strong enough, the vehicle will skid. Also, note that friction acts downwards along the road, as the tendency of the car is to skid up.
Recently Updated Pages
JEE General Topics in Chemistry Important Concepts and Tips

JEE Extractive Metallurgy Important Concepts and Tips for Exam Preparation

JEE Atomic Structure and Chemical Bonding important Concepts and Tips

JEE Amino Acids and Peptides Important Concepts and Tips for Exam Preparation

Electricity and Magnetism Explained: Key Concepts & Applications

JEE Energetics Important Concepts and Tips for Exam Preparation

Trending doubts
JEE Main 2026: City Intimation Slip Releasing Today, Application Form Closed, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

How to Convert a Galvanometer into an Ammeter or Voltmeter

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Hybridisation in Chemistry – Concept, Types & Applications

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

JEE Advanced 2026 - Exam Date (Released), Syllabus, Registration, Eligibility, Preparation, and More

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




